题目内容
已知△ABC的三个顶点的坐标为A(1,1),B(3,2),C(5,4)
(1)求边AB上的高所在直线的方程;
(2)若直线l与AC平行,且在x轴上的截距比在y轴上的截距大1,求直线l与两条坐标轴围成的三角形的周长.
(1)求边AB上的高所在直线的方程;
(2)若直线l与AC平行,且在x轴上的截距比在y轴上的截距大1,求直线l与两条坐标轴围成的三角形的周长.
考点:直线的截距式方程,直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:(1)利用相互垂直的直线斜率之间的关系可得边AB上的高所在直线的斜率,再利用点斜式即可得出;
(2)设直线l的方程为:
+
=1,即y=-
x+a,利用斜率计算公式可得kAC=
,再利用相互平行的直线斜率相等的性质可得-
=
,解得即可.
(2)设直线l的方程为:
| x |
| a+1 |
| y |
| a |
| a |
| a+1 |
| 3 |
| 4 |
| a |
| a+1 |
| 3 |
| 4 |
解答:
解:(1)∵kAB=
,
∴边AB上的高所在直线的斜率为-2,
又∵直线过点C(5,4),
∴直线的方程为:y-4=-2(x-5),即2x+y-14=0.
(2)设直线l的方程为:
+
=1,即y=-
x+a,
∵kAC=
,∴-
=
,解得:a=-
,
∴直线l的方程为:
+
=1.
∴直线l过点(
,0),(0,-
),三角形斜边长为
=
∴直线l与坐标轴围成的直角三角形的周长为
+
+
=
.
| 1 |
| 2 |
∴边AB上的高所在直线的斜率为-2,
又∵直线过点C(5,4),
∴直线的方程为:y-4=-2(x-5),即2x+y-14=0.
(2)设直线l的方程为:
| x |
| a+1 |
| y |
| a |
| a |
| a+1 |
∵kAC=
| 3 |
| 4 |
| a |
| a+1 |
| 3 |
| 4 |
| 3 |
| 7 |
∴直线l的方程为:
| x | ||
|
| y | ||
-
|
∴直线l过点(
| 4 |
| 7 |
| 3 |
| 7 |
(
|
| 5 |
| 7 |
∴直线l与坐标轴围成的直角三角形的周长为
| 5 |
| 7 |
| 4 |
| 7 |
| 3 |
| 7 |
| 12 |
| 7 |
点评:本题综合考查了相互垂直的直线斜率之间的关系、相互平行的直线斜率之间的关系、直线的方程、两点之间的距离公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
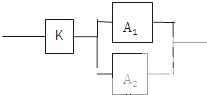 如图.用K,A1,A2分别不同的原件连接成一个系统.当K正常工作且A1和A2正常工作的概率是0.9,0.8,0.8则系统正常工作的概率为( )
如图.用K,A1,A2分别不同的原件连接成一个系统.当K正常工作且A1和A2正常工作的概率是0.9,0.8,0.8则系统正常工作的概率为( )| A、0.960 | B、0.864 |
| C、0.72 | D、0.576 |