题目内容
求方程x2+2x+
=0近似解（精确到0.1）．
| 1 |
| x |
考点：二分法求方程的近似解
专题：函数的性质及应用
分析：直接由计算器求出区间（-3，-2）的端点出的函数值及其区间中点处的函数值，直至区间端点差的绝对值满足精确度为止，则答案可求．
解答：
解：f（-3）=（-3）2+2（-3）-
=2.6667＞0，而f（-2）=（-2）2+2（-2）-
=-0.5＜0．
利用二分法求函数f（x）=x2+2x+
在区间（-3，-2）内的零点的过程如下表：
从上表可以看出，区间[-2.25，-2.21875]内的所有值，若精确到0.1，都是-2.2，所以-2.2是函数f（x）=x2+2x+
在区间（-3，-2）内的零点．
| 1 |
| 3 |
| 1 |
| 2 |
利用二分法求函数f（x）=x2+2x+
| 1 |
| x |
| 左端点 | 右端点 | 中点 | 左端点函数值 | 右端点函数值 | 中间端点函数值 |
| -3 | -2 | -2.5 | 2.6667 | -0.5 | 0.58 |
| -2.5 | -2 | -2.25 | 0.58 | -0.5 | 0.118 |
| -2.25 | -2 | -2.215 | 0.118 | -0.5 | -0.2049 |
| -2.25 | -2.125 | -2.1875 | 0.118 | -0.2049 | -0.0469866 |
| -2.25 | -2.21875 | -2.21875 | 0.118 | -0.0469866 | 4.957498087 |
| 1 |
| x |
点评：本题主要考查用二分法求区间根的问题，本题计算量比较大，解题过程需要细心，属于中档题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
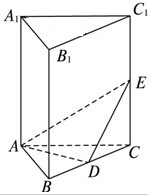已知在直三棱柱ABC-A1B1C1中，E为CC1上任意一点，D在BC上（点D不同于点C），AD⊥DE，求证：平面ADE⊥平面BCC1B1．下列函数中，为奇函数的是（ ）
A、f（x）=
| ||
| B、f（x）=lnx | ||
| C、f（x）=2π | ||
| D、f（x）=sinx |
不等式||x|-1|≤2的解集为（ ）
| A、[-3，3] |
| B、[-1，3] |
| C、[-3，1] |
| D、[-1，1] |