��Ŀ����
2����ͼ1��ֱ������ABCD��AD��BC����BAD=90�㣬EF��AB�����ı���CDFE��EF����ʹDF��AF��BD��ƽ��ABEF���ɽ�Ϊ45�㣬DF=2CE=2��AB=$\sqrt{2}$����ͼ2
��1����֤��AE��ƽ��BDF
��2����$\overrightarrow{AM}$=��$\overrightarrow{AF}$���ˡ�[0��1]���Ƿ���ڷ��������ĵ�M��ʹ��C-BD-MΪֱ����ǣ������ڣ������Ӧ�Ħ�ֵ������˵�����ɣ�
���� ��1���Ƶ���EF��DF��DF��AF���Ӷ�DF��ƽ��ABEF������DF��BF��DF��AE���ɴ˵õ��ı���ABEFΪ�����Σ��Ӷ�AE��BF���ɴ���֤��AE��ƽ��BDF��
��2����FΪ����ԭ�㣬FE��FA��FD����ֱ�߷ֱ�Ϊx�ᣬy�ᣬz�ᣬ�����ռ�ֱ������ϵ��������������������ڷ��������ĵ�Mʹ��C-BD-MΪֱ����ǣ��Ҧ�=1��
��� ֤������1������֪��ֱ������ABCD�У�EF��AB����EF��DF��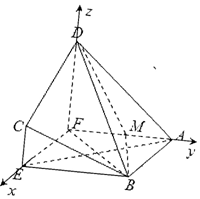
��DF��AF����DF��ƽ��ABEF����DF��BF��DF��AE��
��BD��ƽ��ABEF���ɽ�Ϊ45�㣬��DF=BF=2��
��Rt��BEF�У�BE=$\sqrt{B{F}^{2}-A{B}^{2}}$=$\sqrt{2}$�����ı���ABEFΪ�����Σ�
��AE��BF����AE��ƽ��BDF������5�֣�
�⣺��2����FΪ����ԭ�㣬FE��FA��FD����ֱ�߷ֱ�Ϊx�ᣬy�ᣬz�ᣬ�����ռ�ֱ������ϵ����ͼ��
��F��0��0��0����A��0��$\sqrt{2}$��0����B��$\sqrt{2}��\sqrt{2}$��0��C��$\sqrt{2}$��0��1����D��0��0��2��������6�֣�
$\overrightarrow{BM}$=$\overrightarrow{BA}+\overrightarrow{AM}$=��-$\sqrt{2}$��0��0��+�ˣ�0��-$\sqrt{2}$��0��=��-$\sqrt{2}��-\sqrt{2}�ˣ�0$����
$\overrightarrow{BD}$=��-$\sqrt{2}��-\sqrt{2}��2$����$\overrightarrow{DC}$=��$\sqrt{2}��0��-1$��������7�֣�
��ƽ��BCD��һ��������Ϊ$\overrightarrow{m}$=��x��y��z����ƽ��BDM��һ��������Ϊ$\overrightarrow{n}$=��a��b��c����
��$\left\{\begin{array}{l}{\overrightarrow{BD}•\overrightarrow{m}=\sqrt{2}x+\sqrt{2}y-2z=0}\\{\overrightarrow{DC}•\overrightarrow{m}=\sqrt{2}x-z=0}\end{array}\right.$����x=1����$\overrightarrow{m}$=��1��1��$\sqrt{2}$��������8�֣�
$\left\{\begin{array}{l}{\overrightarrow{BM}•\overrightarrow{n}=a+��b=0}\\{\overrightarrow{BD}•\overrightarrow{n}=\sqrt{2}a+\sqrt{2}b-2c=0}\end{array}\right.$����a=-�ˣ���$\overrightarrow{n}$=��-$�ˣ�1��\frac{\sqrt{2}-\sqrt{2}��}{2}$��������10�֣�
��$\overrightarrow{m}•\overrightarrow{n}$=0����-$��+1+\frac{\sqrt{2}-\sqrt{2}��}{2}��\sqrt{2}=0$����æ�=1��[0��1]������11�֣�
���Դ��ڷ��������ĵ�Mʹ��C-BD-MΪֱ����ǣ��Ҧ�=1������12�֣�
���� ���⿼�����洹ֱ��֤����������������Ϊֱ����ǵĵ��ȷ����������ռ������ߡ����桢������λ�ù�ϵ�Ȼ���֪ʶ������������֤����������������������黯����ת��˼�롢�����뷽��˼�룬���е��⣮

 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�| A�� | ��Ҫ���� | B�� | �Ȳ����Ҳ����Ҫ���� | ||
| C�� | ������� | D�� | ��Ҫ���� |
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{2}{5}$ |
| A�� | 30 | B�� | 31 | C�� | 62 | D�� | 63 |
| A�� | 2 | B�� | -2 | C�� | 1 | D�� | -1 |
��1������ӵ�8�е�7�е�����ʼ���Ҷ�����������д�����ȼ���3���˵ı�ţ�
������ժȡ�˵�7�е���9�У�
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
��2����ȡ��100�˵���ѧ�������ˮƽ���Գɼ����±���
�ɼ���Ϊ���㡢���á����������ȼ�����������ֱ��ʾ�����ɼ�����ѧ�ɼ������磺������ѧ�ɼ�Ϊ���õĹ���20+18+4=42
�����ڸ������У���ѧ�ɼ���������30%����a��b��ֵ��
| ���� | ��ѧ | |||
| ���� | ���� | ���� | ||
| ���� | ���� | 7 | 20 | 5 |
| ���� | 9 | 18 | 6 | |
| ���� | a | 4 | b | |