题目内容
7.在区间[-1,1]上任取两数a、b,则使关于x的二次方程${x^2}+2\sqrt{{a^2}+{b^2}}x+1=0$有实数根的概率为$1-\frac{π}{4}$.分析 根据二次方程根的个数与△的关系,我们易得到关于x的二次方程x2+2 $\sqrt{{a}^{2}{+b}^{2}}$x+1=0的两根都是实数?a2+b2≥1,分别求出在区间[-1,1]上任取两数a、b,对应的平面区域面积,和满足a2+b2≥1对应的平面区域面积,代入几何概型概率计算公式,即可得到答案.
解答 解:若关于x的二次方程x2+2$\sqrt{{a}^{2}{+b}^{2}}$x+1=0的两根都是实数,
则△=4(a2+b2)-4≥0,即a2+b2≥1,
在区间[-1,1]上任取两数a、b对应的平面区域如下图中矩形面积所示,
其中满足条件a2+b2≥1的点如下图中阴影部分所示,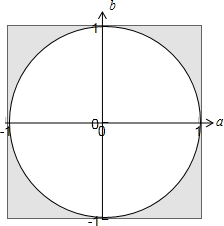
∵S矩形=2×2=4,S阴影=4-π
故在区间[-1,1]上任取两数a、b,
则使关于x的二次方程x2+2$\sqrt{{a}^{2}{+b}^{2}}$x+1=0的两根都是实数的概率P=$\frac{{S}_{阴影}}{{S}_{矩形}}$=1-$\frac{π}{4}$,
故答案为:1-$\frac{π}{4}$.
点评 本题考查的知识点是几何概型,其中分析出关于x的二次方程x2+2$\sqrt{{a}^{2}{+b}^{2}}$x+1=0的两根都是实数?a2+b2≥1是解答本题的关键.

练习册系列答案
相关题目
17.已知α,β∈R,则“α>β”是“α-β>sinα-sinβ”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
15.已知${log_{\frac{1}{2}}}a<{log_{\frac{1}{2}}}b$,则下列不等式一定成立的是( )
| A. | ${({\frac{1}{4}})^a}<{({\frac{1}{3}})^b}$ | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ln(a-b)>0 | D. | 3a-b<1 |
2.已知双曲线$\frac{x^2}{2}-\frac{y^2}{a^2}=1$过点(2,-1),则该双曲线的渐近线方程为( )
| A. | $y=±\frac{{\sqrt{2}}}{2}x$ | B. | $y=±\sqrt{2}x$ | C. | y=±x | D. | $y=±\frac{{\sqrt{5}}}{2}x$ |
17.已知中心在坐标原点的双曲线的一个焦点与抛物线y=-$\frac{1}{4}$x2的焦点重合,且双曲线的离心率等于$\sqrt{5}$,则该双曲线的渐近线方程为( )
| A. | y=±2x | B. | y=±$\frac{2\sqrt{5}}{5}$x | C. | y=±$\frac{\sqrt{5}}{2}$x | D. | y=±$\frac{1}{2}$x |
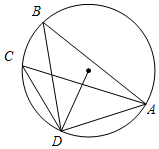 如图,圆内接四边形ABCD中,AD=DC=2BC=2,AB=3.
如图,圆内接四边形ABCD中,AD=DC=2BC=2,AB=3.