题目内容
8.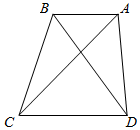 如图,梯形ABCD中,AB∥CD,BC=6,tan∠ABC=-2$\sqrt{2}$.
如图,梯形ABCD中,AB∥CD,BC=6,tan∠ABC=-2$\sqrt{2}$.(I)若∠ACD=$\frac{π}{4}$,求AC的长;
(Ⅱ)若BD=9,求△BCD的面积.
分析 (Ⅰ)由同角的三角函数的关系求出sin∠ABC=$\frac{2\sqrt{2}}{3}$,由正弦定理即可求出AC,
(Ⅱ)分别利用正弦定理和余弦定理和三角形的面积公式即可求出.
解答 解:(Ⅰ):∵AB∥CD,∠ACD=$\frac{π}{4}$,
∴∠BAC=∠ACD=$\frac{π}{4}$,
∵tan∠ABC=-2$\sqrt{2}$,
∴sin∠ABC=-2$\sqrt{2}$cos∠ABC,
∵sin2∠ABC+cos2∠ABC=1,
∴sin∠ABC=$\frac{2\sqrt{2}}{3}$,
由正弦定理可得$\frac{BC}{sin∠BAC}$=$\frac{AC}{sin∠ABC}$,
∴$\frac{6}{\frac{\sqrt{2}}{2}}$=$\frac{AC}{\frac{2\sqrt{2}}{3}}$,
∴AC=8,
(Ⅱ)∵AB∥CD,
∴∠BCD=π-∠ABC,
∴sin∠BCD=sin(π-∠ABC)=sin∠ABC=$\frac{2\sqrt{2}}{3}$,
∴cos∠BCD=$\frac{1}{3}$,
由余弦定理可得BD2=BC2+CD2-2BC•CD•cos∠BCD,
即81=36+CD2-2×6×CD×$\frac{1}{3}$,
解得CD=9
∴S△BCD=$\frac{1}{2}$CD•BCsin∠BCD=$\frac{1}{2}$×6×9×$\frac{2\sqrt{2}}{3}$=18$\sqrt{2}$.
点评 本题考查了同角的三角函数的关系和正弦定理和余弦定理以及面积公式,属于基础题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
18.函数f(x)=(x+1)ex在点(0,1)处的切线方程为( )
| A. | 2x-y-1=0 | B. | 2x-y+1=0 | C. | x-2y-1=0 | D. | x-2y+1=0 |
19.下列函数中既是奇函数,又在区间(0,+∞)内是增函数的为( )
| A. | y=sinx,x∈R | B. | y=ln|x|,x∈R,且x≠0 | C. | y=x3,x∈R | D. | y=x2,x∈R |
3.方程$\left\{\begin{array}{l}{x=1+sinθ}\\{y=sin2θ}\end{array}\right.$(θ是参数)所表示曲线经过下列点中的( )
| A. | (1,1) | B. | ($\frac{2}{3}$,$\frac{1}{2}$) | C. | ($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$) | D. | ($\frac{2+\sqrt{3}}{2}$,-$\frac{1}{2}$) |