题目内容
20.已知函数f(x)=$\sqrt{3}$cos2ωx+sinωxcosωx(ω>0)的周期为π.(1)当x∈[0,$\frac{π}{2}$]时,求函数f(x)的值域;
(2)已知△ABC的内角A,B,C对应的边分别为a,b,c,若f($\frac{A}{2}$)=$\sqrt{3}$,且a=4,b+c=5,求△ABC的面积.
分析 (1)利用三角函数恒等变换的应用化简可得f(x)=sin(2ωx+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$,利用周期公式可求ω,可得f(x)的解析式,由x∈[0,$\frac{π}{2}$],可得:sin(2x+$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,1],即可求值函数值域.
(2)由f($\frac{A}{2}$)=$\sqrt{3}$,结合范围A+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{4π}{3}$),解得A的值,由余弦定理可得bc的值,利用三角形面积公式即可求值得解.
解答 解:(1)∵f(x)=$\sqrt{3}$cos2ωx+sinωxcosωx=$\sqrt{3}$×$\frac{1+cos2ωx}{2}$+$\frac{1}{2}$sin2ωx=sin(2ωx+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$,
∴由题意可得:$\frac{2π}{2ω}$=π,解得:ω=1,可得:f(x)=sin(2x+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$.
∵x∈[0,$\frac{π}{2}$],
∴2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],可得:sin(2x+$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,1],
∴f(x)=sin(2x+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$∈[0,$\frac{\sqrt{3}}{2}$+1].
(2)∵f($\frac{A}{2}$)=sin(A+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,A+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{4π}{3}$),
∴A+$\frac{π}{3}$=$\frac{2π}{3}$,解得:A=$\frac{π}{3}$.
∴由余弦定理a2=b2+c2-2bccosA,可得:16=b2+c2-bc=(b+c)2-3bc=25-3bc,解得:bc=3,
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×3×$$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$.
点评 本题主要考查了三角函数恒等变换的应用,周期公式,正弦函数的图象和性质,余弦定理,三角形面积公式在解三角形中的应用,属于中档题.

 在如图的正方体中,E、F分别为棱AB和棱AA1的中点,点M、N分别为线段D1E、C1F上的点,则与平面ABCD平行的直线MN有( )条.
在如图的正方体中,E、F分别为棱AB和棱AA1的中点,点M、N分别为线段D1E、C1F上的点,则与平面ABCD平行的直线MN有( )条.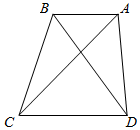 如图,梯形ABCD中,AB∥CD,BC=6,tan∠ABC=-2$\sqrt{2}$.
如图,梯形ABCD中,AB∥CD,BC=6,tan∠ABC=-2$\sqrt{2}$.