题目内容

18．函数f（x）=（x+1）ex在点（0，1）处的切线方程为（　　）
A．2x-y-1=0B．2x-y+1=0C．x-2y-1=0D．x-2y+1=0

分析 求函数的导数，利用导数的几何意义即可得到结论．

解答 解：函数的导数f′（x）=ex+（x+1）ex=（x+2）ex，
则f′（0）=2，
即函数f（x）在点（0，1）处的切线斜率k=f′（0）=2，
则对应的切线方程为y-1=2x，即2x-y+1=0，
故选：B

点评 本题主要考查函数切线的求解，根据导数的几何意义是解决本题的关键．比较基础．

练习册系列答案
相关题目
8．已知函数f（x）=ex+ax+b（a，b∈R，e是自然对数的底数）在点（0，1）处的切线与x轴平行．
（Ⅰ）求a，b的值；
（Ⅱ）若对一切x∈R，关于x的不等式f（x）≥（m-1）x+n恒成立，求m+n的最大值．
9．命题p：$\frac{x^2}{a-2}-\frac{y^2}{6-a}=1$是双曲线的方程；命题q：函数f（x）=（5-a）x在R上为增函数．若p∨q为真，p∧q为假，求实数a的取值范围．
6．三棱锥P-ABC四个顶点都在球O上，已知PA⊥AB，PA⊥AC，PA=2，BC=3，∠BAC=60°，则球O的体积是$\frac{32π}{3}$．
13．将编号为1，2，3，4的四个小球放入3个不同的盒子中，每个盒子里至少放1个，则恰有1个盒子放有2个连号小球的所有不同放法有18种．（用数字作答）
3．若$sin（π+α）=\frac{1}{3}$，则sinα=（　　）
A．$\frac{1}{3}$B．$-\frac{1}{3}$C．3D．-3
10．已知角α的终边经过P（3，4），求sinα，cosα，tanα．
7．下列说法正确的序号是②④．
①第一象限角是锐角；
②函数$y={log_{\frac{1}{2}}}（{{x^2}+2x-3}）$的单调增区间为（-∞，-3）；
③函数f（x）=|cosx|是周期为2π的偶函数；
④方程$x=tanx{，_{\;}}x∈（{-\frac{π}{2}，\frac{π}{2}}）$只有一个解x=0．
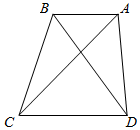8．如图，梯形ABCD中，AB∥CD，BC=6，tan∠ABC=-2$\sqrt{2}$．
（I）若∠ACD=$\frac{π}{4}$，求AC的长；
（Ⅱ）若BD=9，求△BCD的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网