题目内容
设x,y为正实数,且x+2y=1,则
+
的最小值为 .
| 1 |
| x |
| 1 |
| y |
考点:基本不等式
专题:不等式的解法及应用
分析:利用“乘1法”和基本不等式即可得出.
解答:
解:∵x,y为正实数,且x+2y=1,∴
+
=(x+2y)(
+
)=3+
+
≥3+2
=3+2
.当且仅当x=
y=
-1时取等号.
∴
+
的最小值为3+2
.
故答案为3+2
.
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
| 2y |
| x |
| x |
| y |
|
| 2 |
| 2 |
| 2 |
∴
| 1 |
| x |
| 1 |
| y |
| 2 |
故答案为3+2
| 2 |
点评:熟练掌握“乘1法”和基本不等式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)是定义在R上的奇函数,当x≤0时f(x)=x-cosx,则f(1)=( )
| A、-1+cos1 |
| B、1-cos1 |
| C、-1-cos1 |
| D、1+cos1 |
若f(x)=x2+6,x∈[-1,2],则f(x)是( )
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数,又是偶函数 |
| D、非奇非偶函数 |
已知变量x,y满足约束条件
,则4x+2y的取值范围是( )
|
| A、[0,10] |
| B、[0,12] |
| C、[2,10] |
| D、[2,12] |
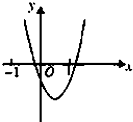 二次函数y=ax2+bx+c的图象如图所示,反比例函数y=
二次函数y=ax2+bx+c的图象如图所示,反比例函数y=