题目内容
已知A、B、C、D是表面积为6π的球O上的四点,且DA⊥平面ABC,△ABC是∠B=90°的等腰直角三角形,且AC=2,则VD-ABC的体积为 .
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:确定DC是球O直径,利用球O的表面积为6π,求出CD,利用△ABC是∠B=90°的等腰直角三角形,AC=2,可得S△ABC=1,即可求出VD-ABC.
解答:
解:因为DA⊥平面ABC,△ABC是∠B=90°的等腰直角三角形,
所以DC是球O直径,
因为球O的表面积为6π,所以R=
,
所以CD=
,
因为AC=2,
所以AD=
,
因为△ABC是∠B=90°的等腰直角三角形,AC=2,
所以S△ABC=1
所以VD-ABC=
×1×
=
.
故答案为:
.
所以DC是球O直径,
因为球O的表面积为6π,所以R=
| ||
| 2 |
所以CD=
| 6 |
因为AC=2,
所以AD=
| 2 |
因为△ABC是∠B=90°的等腰直角三角形,AC=2,
所以S△ABC=1
所以VD-ABC=
| 1 |
| 3 |
| 2 |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查棱锥的体积,考查球的表面积公式,考查学生的计算能力,确定DC是球O直径是关键.

练习册系列答案
相关题目
设函数y=f(x)的定义域是(0,1),则函数y=f(x2)的定义域是( )
| A、(0,1) |
| B、(-1,1) |
| C、(-1,0) |
| D、(-1,0)∪(0,1) |
设非负实数x,y满足x-y+1≥0且3x+y-3≤0,则4x+y的最大值为( )
| A、1 | ||
B、
| ||
C、
| ||
| D、4 |
 如图,分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域,若向该正方形内随机投一点,则该点落在空白区域的概率为( )
如图,分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域,若向该正方形内随机投一点,则该点落在空白区域的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
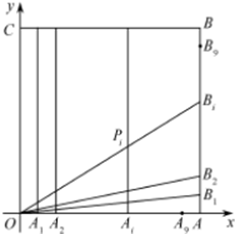 如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点Pi(i∈N*,1≤i≤9).
如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点Pi(i∈N*,1≤i≤9).