题目内容
4.函数$f(x)={log_{\frac{1}{2}}}({2-x})$的单调递增区间为(-∞,2).分析 令t=2-x>0,求得函数的定义域为(-∞,2),则f(x)=g(t)=${log}_{\frac{1}{2}}t$,本题即求函数t的减区间,利用一次函数的性质得出结论.
解答 解:令t=2-x>0,求得x<2,故函数的定义域为(-∞,2),则f(x)=g(t)=${log}_{\frac{1}{2}}t$,
故本题即求函数t的减区间,而一次函数t在其定义域(-∞,2)内单调递减,
故答案为:(-∞,2).
点评 本题主要考查复合函数的单调性,对数函数、一次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
6.设复数z=1-i(i是虚数单位),则$\frac{2}{z}$+z等于( )
| A. | 2 | B. | -2 | C. | 2i | D. | -2i |
14.下列命题中,为真命题的是( )
| A. | ?x0∈R,使得${e^{x_0}}≤0$ | |
| B. | $sinx+\frac{1}{sinx}≥2(x≠kπ,k∈Z)$ | |
| C. | ?x∈R,2x>x2 | |
| D. | 若命题p:?x0∈R,使得$x_0^2-{x_0}+1<0$,则¬p:?x0∈R,都有x2-x+1≥0 |
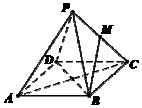 如图,已知正四棱锥P-ABCD中,AB=4,高$h=2\sqrt{2}$,点M是侧棱PC的中点,则异面直线BM与AC所成角的余弦值为$\frac{\sqrt{6}}{6}$.
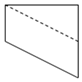
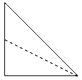
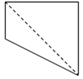
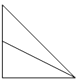
如图,已知正四棱锥P-ABCD中,AB=4,高$h=2\sqrt{2}$,点M是侧棱PC的中点,则异面直线BM与AC所成角的余弦值为$\frac{\sqrt{6}}{6}$.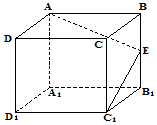 如图,正方体ABCD-A1B1C1D1中,E为棱BB1的中点,用过点A、E、C1的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是( )
如图,正方体ABCD-A1B1C1D1中,E为棱BB1的中点,用过点A、E、C1的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是( )