题目内容
4.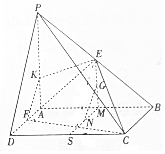 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,点E,F,M,S分别为棱PB,AD,AB,CD的中点,G为线段EM的中点,且PA=AB=2AD=4,N为SM上一点,且NG∥平面CEF.
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,点E,F,M,S分别为棱PB,AD,AB,CD的中点,G为线段EM的中点,且PA=AB=2AD=4,N为SM上一点,且NG∥平面CEF.(1)确定N的位置,并求线段NG的长;
(2)平面CEF与PA交于点K,求三棱锥B-CKN的体积.
分析 (1)设CF与SM交于点O,连结OE,则N为OM的中点.从而EM∥PA,进而EM⊥底面ABCD,由此能求出NG的长.
(2)延长CF交BA的延长线于点Q,连结EQ,则点K为PA与QE的交点,由题意△AKQ∽△MEQ,由此能求出三棱锥B-CKN的体积.
解答 解:(1)设CF与SM交于点O,连结OE,则N为OM的中点.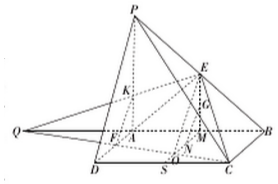
证明如下:
∵NG∥平面CEF,且平面CEF∩平面MOE=EO,
∴NG∥OE,又G为线段EM的中点,则N为OM的中点,
∵E为棱PB的中点,∴EM∥PA,
又PA⊥底面ABCD,∴EM⊥底面ABCD,
则EM⊥OM,∵OM=$\frac{1+2}{2}=\frac{3}{2}$,EM=2,
∴NG=$\frac{1}{2}OE$=$\frac{1}{2}\sqrt{O{M}^{2}+E{M}^{2}}$=$\frac{5}{4}$.
(2)延长CF交BA的延长线于点Q,
∵AF∥BC,且BC=2AF,∴A为QB的中点,
连结EQ,则点K为PA与QE的交点,
由题意△AKQ∽△MEQ,∴$\frac{AK}{EM}=\frac{QA}{QM}=\frac{4}{4+2}=\frac{2}{3}$,
∴AK=$\frac{2}{3}EM=\frac{4}{3}$,
∵△BCN的面积为$\frac{1}{2}×2×2=2$,
∴三棱锥B-CKN的体积VB-CKN=VK-BCN=$\frac{1}{3}×AK×2=\frac{8}{9}$.
点评 本题考查点的位置的确定,考查线段长的求法,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
18.某质点运动的距离y与时间t的关系为y=t+lnt,那么这个质点在t=1时的瞬时速度为( )
| A. | e | B. | 2 | C. | 1 | D. | $\frac{1}{e}$ |
9.“x>1”是“x>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
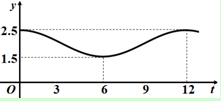 某企业一天中不同时刻的用电量y(万千瓦时)关于时间t(小时,0≤t≤24)的函数y=f(t)近似满足f(t)=Asin(ωt+φ)+B,(A>0,ω>0,0<φ<π).如图是函数y=f(t)的部分图象(t=0对应凌晨0点).
某企业一天中不同时刻的用电量y(万千瓦时)关于时间t(小时,0≤t≤24)的函数y=f(t)近似满足f(t)=Asin(ωt+φ)+B,(A>0,ω>0,0<φ<π).如图是函数y=f(t)的部分图象(t=0对应凌晨0点).