题目内容
已知在△ABC中,AB=4,AC=2,若|λ
+(2-2λ)
|的最小值是2,则对于△ABC内一点P,则
•(
+
)的最小值是 .
| AB |
| AC |
| PA |
| PB |
| PC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:|λ
+(2-2λ)
|=
=4
=f(λ).当cosA=0时,f(λ)=4
≥2
,舍去.当cosA≠0时,f(λ)
=4
≥4
=2,解得A=
.如图所示建立直角坐标系,A(0,0),B(4,0),C(-1,
).设P(x,y),可得
•(
+
)=2(x-
)2+2(y-
)2-
,即可得出.
| AB |
| AC |
λ2
|
| (2-2cosA)λ2+(2cosA-2)λ+1 |
| 2λ2-2λ+1 |
| 2 |
=4
(2-2cosA)(λ-
|
|
| 2π |
| 3 |
| 3 |
| PA |
| PB |
| PC |
| 3 |
| 4 |
| ||
| 4 |
| 3 |
| 2 |
解答:
解:|λ
+(2-2λ)
|=
=
=4
=f(λ).
当cosA=0时,f(λ)=4
=4
≥2
,舍去.
当cosA≠0时,f(λ)=4
≥4
=2,解得cosA=-
,
∴A=
.
如图所示建立直角坐标系,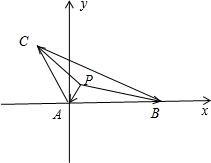 A(0,0),B(4,0),C(-1,
A(0,0),B(4,0),C(-1,
).
设P(x,y),则
+
=(-1-x,
-y)+(4-x,-y)
=(3-2x,
-2y).
=(-x,-y).
∴
•(
+
)=(-x,-y)•(3-2x,
-2y)
=-x(3-2x)-y(
-2y)
=2(x-
)2+2(y-
)2-
≥-
,
当x=
,y=
时(此时点P在△ABC内部)取得最小值-
.
故答案为:-
.
| AB |
| AC |
λ2
|
=
| 16λ2+4(2-2λ)2+2λ(2-2λ)×8cosA |
=4
| (2-2cosA)λ2+(2cosA-2)λ+1 |
当cosA=0时,f(λ)=4
| 2λ2-2λ+1 |
2(λ-
|
| 2 |
当cosA≠0时,f(λ)=4
(2-2cosA)(λ-
|
|
| 1 |
| 2 |
∴A=
| 2π |
| 3 |
如图所示建立直角坐标系,
 A(0,0),B(4,0),C(-1,
A(0,0),B(4,0),C(-1,| 3 |
设P(x,y),则
| PC |
| PB |
| 3 |
=(3-2x,
| 3 |
| PA |
∴
| PA |
| PB |
| PC |
| 3 |
=-x(3-2x)-y(
| 3 |
=2(x-
| 3 |
| 4 |
| ||
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
当x=
| 3 |
| 4 |
| ||
| 4 |
| 3 |
| 2 |
故答案为:-
| 3 |
| 2 |
点评:本题考查了向量的三角形法则、向量的数量积运算性质、二次函数的单调性、分类讨论的思想方法,考查了推理能力与计算能力,考查了数形结合的思想方法,属于难题.

练习册系列答案
相关题目
将函数y=sin
x的图象向右平移2个单位后,得到函数f(x)的图象,则函数f(x)的单调递减区间是( )
| π |
| 2 |
| A、[-1+2k,1+2k],k∈Z | ||||
| B、[1+4k,3+4k],k∈Z | ||||
| C、[-1+4k,1+4k],k∈Z | ||||
D、[-1+4k+
|
如图所示,程序框图(算法流程图)的输出结果是( )


| A、9 | B、23 | C、49 | D、53 |
在△ABC中,c=acosB,b=asinC,则△ABC一定是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等边三角形 |
| D、等腰直角三角形 |
已知l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )
| A、若l⊥α,m?α,则l⊥m |
| B、若l⊥m,m?α,则l⊥α |
| C、若l∥α,m?α,则l∥m |
| D、若l∥α,m∥α,则l∥m |
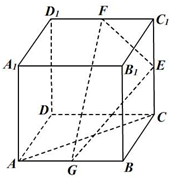 如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.