题目内容

11．函数y=$\frac{1}{\sqrt{1-x}}$的定义域为（　　）
A．（0，1]B．（-∞，1）C．（-∞，1]D．（1，+∞）

分析 由分母中根式内部的代数式大于0求得x的范围得答案．

解答 解：要使原函数有意义，则1-x＞0，即x＜1．
∴函数y=$\frac{1}{\sqrt{1-x}}$的定义域为（-∞，1）．
故选：B．

点评 本题考查函数的定义域及其求法，是基础的计算题．

练习册系列答案
相关题目
1．在复平面内，复数z=i（1+i），那么|z|=（　　）
A．1B．$\sqrt{2}$C．$\sqrt{3}$D．2
2．设x∈R，“x＞1“的一个充分条件是（　　）
A．x＞-1B．x≥0C．x≥1D．x＞2
19．函数f（x）=$\sqrt{-1+lnx}$的定义域是[e，+∞）．
6．函数f（x）=xm（1-x）n在区间[0，1]上的图象如图所示，则m，n的值为（　　）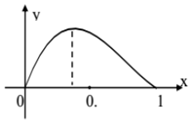
A．m=1，n=1B．m=1，n=2C．m=2，n=1D．m=2，n=2
16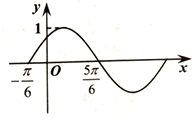．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则关于f（x）的说法正确的是（　　）
A．对称轴方程是x=$\frac{π}{3}$+2kπ（k∈Z）B．φ=-$\frac{π}{6}$
C．最小正周期为πD．在区间（$\frac{π}{2}$，$\frac{7π}{6}$）上单调递减
3．已知函数f（x）=cosωx（ω＞0），将y=f（x）的图象向右平移$\frac{π}{3}$个单位长度后，所得的图象与原图象重合，则ω的最小值为（　　）
A．3B．6C．9D．12
20．已知F1（-3，0），F2（3，0），动点P满足|PF1|-|PF2|=4，则点P的轨迹是（　　）
A．双曲线B．双曲线的一支C．一条射线D．不存在
1．过点A（2，1），且与直线x+2y-1=0垂直的直线方程为（　　）
A．x+2y-4=0B．x-2y=0C．2x-y-3=0D．2x+y-5=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网