题目内容
12.过点A(-6,10)且与直线l:x+3y+16=0相切于点B(2,-6)的圆的方程是x2+y2-12x-12y-88=0.分析 设所求圆的方程为x2+y2+Dx+Ey+F=0,利用条件建立3个方程,求出D,E,F,即可得出结论.
解答 解:设所求圆的方程为x2+y2+Dx+Ey+F=0,
则圆心C($\frac{D}{2}$,$\frac{E}{2}$).∴kCB=$\frac{-6-\frac{E}{2}}{2-\frac{D}{2}}$,由kCB•kl=-1,得
$\frac{-6-\frac{E}{2}}{2-\frac{D}{2}}$•(-$\frac{1}{3}$)=-1,①
又有(-6)2+102-6D+10E+F=0,②
22+(-6)2+2D-6E+F=0.③
由①②③联立可得D=-12,E=-12,F=-88.
∴圆的方程为x2+y2-12x-12y-88=0.
点评 本题考查圆的方程的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
相关题目
3.设函数$f(x)=\left\{\begin{array}{l}{log_2}(-x),x<0\\{2^x},x≥0\end{array}\right.$,若关于x的方程f2(x)-af(x)=0恰有三个不同的实数根,则实数a的取值范围是( )
| A. | [0,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | [1,+∞) |
20.已知圆C的圆心与点P(-2,1)关于直线y=x+1对称,直线3x+4y-11=0与圆C相交于A,B点,且|AB|=6,则圆C的方程为( )
| A. | x2+(y+1)2=18 | B. | (x+1)2+y2=9 | C. | (x+1)2+y2=18 | D. | x2+(y+1)2=9 |
7.设$({x^2}-3){(2x+3)^{2015}}={a_0}+{a_1}(x+2)+{a_2}{(x+2)^2}+…+{a_{2017}}{(x+2)^{2017}}$,则a1+a2+…+a2017的值为( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
17.如图是一个结构图,在框②中应填入( )
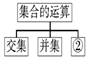

| A. | 空集 | B. | 补集 | C. | 子集 | D. | 全集 |
4.一个几何体的三视图如图所示,则这个几何体的表面积为( )
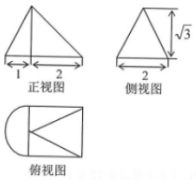

| A. | 8+$\frac{π}{2}$+$\sqrt{7}$ | B. | 8+$\frac{3π}{2}$+$\sqrt{7}$ | C. | 6+$\frac{3π}{2}$+$\sqrt{3}$ | D. | 6+$\frac{π}{2}$+$\sqrt{3}$ |
1.在以“菊韵荆门,荣耀中华”为主题的“中国•荆门菊花展”上,工作人员要将6盆不同品种的菊花排成一排,其中甲,乙在丙同侧的不同排法种数为( )
| A. | 120 | B. | 240 | C. | 360 | D. | 480 |