题目内容
1.抛物线y2=2px(p>0)的焦点为F,过焦点F且倾斜角为$\frac{π}{3}$的直线与抛物线相交于A,B两点,若|AB|=8,则抛物线的方程为( )| A. | y2=4x | B. | y2=8x | C. | y2=3x | D. | y2=6x |
分析 抛物线的方程可求得焦点坐标,进而根据斜率表示出直线的方程,与抛物线的方程联立消去y,进而根据韦达定理表示出x1+x2和x1x2,进而利用配方法求得|x1-x2|,利用弦长公式表示出段AB的长求得p,即可得出结论.
解答 解:由题意可知过焦点的直线方程为y=$\sqrt{3}(x-\frac{p}{2})$,
联立抛物线方程整理可得3x2-5px+$\frac{3}{4}$p2=0,
∴x1+x2=$\frac{5}{3}$p,x1x2=$\frac{{p}^{2}}{4}$,
∴|x1-x2|=$\sqrt{\frac{25}{9}{p}^{2}-{p}^{2}}$=$\frac{4}{3}$p,
又|AB|=$\sqrt{1+3}•\frac{4}{3}p$=8求得p=3,
∴抛物线的方程为y2=6x.
故选D.
点评 本题主要考查了抛物线的应用,两点间的距离公式的应用.解题的时候注意利用好韦达定理,设而不求,找到解决问题的途径.

练习册系列答案
相关题目
10.已知函数$f(x)=lnx+ax-\frac{1}{x}+b$.
(1)若函数$g(x)=f(x)+\frac{2}{x}$为减函数,求a的取值范围;
(2)若f(x)≤0恒成立,证明:a≤1-b.
(1)若函数$g(x)=f(x)+\frac{2}{x}$为减函数,求a的取值范围;
(2)若f(x)≤0恒成立,证明:a≤1-b.
11.设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(1)=( )
| A. | 1 | B. | 3 | C. | -3 | D. | 0 |
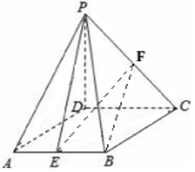 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E、F分别为AB和PC的中点,连接EF、BF.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E、F分别为AB和PC的中点,连接EF、BF.