题目内容
11．设f（x）是定义在R上的奇函数，当x≤0时，f（x）=2x2-x，则f（1）=（ ）| A． | 1 | B． | 3 | C． | -3 | D． | 0 |
分析 由奇函数性质得当x＞0时，f（x）=-2x2-x，由此能求出f（1）．
解答 解：∵f（x）是定义在R上的奇函数，
当x≤0时，f（x）=2x2-x，
∴当x＞0时，f（x）=-2x2-x，
∴f（1）=-2-1=-3．
故选：C．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
相关题目
1．抛物线y2=2px（p＞0）的焦点为F，过焦点F且倾斜角为$\frac{π}{3}$的直线与抛物线相交于A，B两点，若|AB|=8，则抛物线的方程为（ ）
| A． | y2=4x | B． | y2=8x | C． | y2=3x | D． | y2=6x |
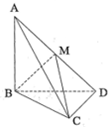如图，三棱锥A-BCD中，AB⊥平面BCD，CD⊥BD．
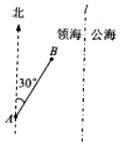一缉私艇巡航至距领海边界线l（一条南北方向的直线）3.8海里的A处，发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑，缉私艇立即追击，已知缉私艇的最大航速是走私船最大航速的3倍，假设缉私艇和走私船均按直线方向以最大航速航行．
3．在△ABC中，角A，B，C的对边分别为a，b，c，且$\frac{cosB}{b}$=-$\frac{3cosC}{c}$，则角A的最大值是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
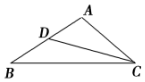如图所示，给出下列条件：
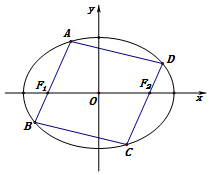已知椭圆E的方程是$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1，左、右焦点分别是F1、F2，在椭圆E上有一动点A，过A、F1作一个平行四边形，使顶点A、B、C、D都在椭圆E上，如图所示．