题目内容
12.我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.问次一尺各重几何?”意思是:“现有一根金杖,长5尺,一头粗,一头细.在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”设该金杖由粗到细是均匀变化的,其重量为M,现将该金杖截成长度相等的10段,记第i段的重量为ai(i=1,2,…,10),且a1<a2<…<a10,若48ai=5M,则i=6.分析 由题意知由细到粗每段的重量成等差数列,记为{an}且设公差为d,由条件和等差数列的通项公式列出方程组,求出a1和d值,由等差数列的前n项和公式求出该金杖的总重量M,代入已知的式子化简求出i的值.
解答 解:由题意知由细到粗每段的重量成等差数列,
记为{an},设公差为d,
则$\left\{\begin{array}{l}{{a}_{1}+{a}_{2}=2}\\{{a}_{9}+{a}_{10}=4}\end{array}\right.$,解得a1=$\frac{15}{16}$,d=$\frac{1}{8}$,
所以该金杖的总重量M=$10×\frac{15}{16}+\frac{10×9}{2}×\frac{1}{8}$=15,
因为48ai=5M,所以48[$\frac{15}{16}$+(i-1)×$\frac{1}{8}$]=25,
即39+6i=75,解得i=6,
故答案为:6.
点评 本题考查等差数列的通项公式、前n项和公式的实际应用,以及方程思想,考查化简、计算能力.

练习册系列答案
相关题目
3.($\sqrt{x}$-$\frac{2}{x}$+1)7的展开式中x3的系数为( )
| A. | -1 | B. | 1 | C. | -7 | D. | 7 |
7.复数z=$\frac{3-2{i}^{3}}{1+i}$的虚部为( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{5}{2}$ | D. | $\frac{1}{2}$ |
4.已知实数x,y满足$\left\{\begin{array}{l}{3x+2y-12≤0}\\{x≥2}\\{y≥\frac{3}{2}}\end{array}\right.$,则$\frac{xy}{{x}^{2}{+y}^{2}}$的取值范围是( )
| A. | [2,$\frac{5}{2}$] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | (0,$\frac{1}{2}$] | D. | [$\frac{2}{5}$,$\frac{1}{2}$] |
1.抛物线y2=2px(p>0)的焦点为F,过焦点F且倾斜角为$\frac{π}{3}$的直线与抛物线相交于A,B两点,若|AB|=8,则抛物线的方程为( )
| A. | y2=4x | B. | y2=8x | C. | y2=3x | D. | y2=6x |
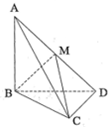 如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.
如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.