题目内容
11.若z=(a-1)+ai为纯虚数,其中a∈R,则$\frac{a+{i}^{7}}{1+ai}$=( )| A. | -i | B. | i | C. | 1+i | D. | 1-i |
分析 利用复数代数形式的乘除运算化简即可得答案.
解答 解:z=(a-1)+ai为纯虚数,
∴a=1,
∴$\frac{1+{i}^{7}}{1+i}$=$\frac{(1-i)(1-i)}{(1+i)(1-i)}$=$\frac{-2i}{2}$=-i,
故选:A
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
1.已知m,n是两条不同的直线,α,β是两个不同的平面,给出下列四个命题,错误的命题是( )
| A. | 若m∥α,m∥β,α∩β=n,则m∥n | B. | 若α⊥β,m⊥α,n⊥β,则m⊥n | ||
| C. | 若α⊥β,α⊥γ,β∩γ=m,则m⊥α | D. | 若α∥β,m∥α,则m∥β |
19.已知抛物线C1:y2=ax(a>0)的焦点与双曲线C2:$\frac{x^2}{4}-\frac{y^2}{b^2}=1({b>0})$的右焦点重合,记为F点,点M与点P(4,6)分别为曲线C1,C2上的点,则|MP|+|MF|的最小值为( )
| A. | $\frac{5}{2}$ | B. | 8 | C. | $\frac{13}{2}$ | D. | $\frac{11}{2}$ |
3.已知复数z满足(1+i)z=|$\sqrt{3}$+i|,i为虚数单位,则z等于( )
| A. | 1-i | B. | 1+i | C. | $\frac{1}{2}$-$\frac{1}{2}$i | D. | $\frac{1}{2}$+$\frac{1}{2}$i |
2.已知集合$A=\left\{{x\left|{y=lg\frac{2-x}{x+2}}\right.}\right\}$,集合B={y|y=1-x2},则集合{x|x∈A∪B且x∉A∩B}为( )
| A. | [-2,1]∪(2,+∞) | B. | (-2,1)∪(2,+∞) | C. | (-∞,-2)∪[1,2) | D. | (-∞,-2]∪(1,2) |
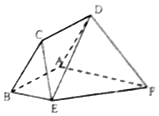 如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$.
如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$.