题目内容
9.已知函数f(x)=|x-4|+|x-2|.(1)求不等式f(x)>2的解集;
(2)设f(x)的最小值为M,若2x+a≥M的解集包含[0,1],求a的取值范围.
分析 (1)f(x)=|x-4|+|x-2|=$\left\{\begin{array}{l}{6-2x.x≤2}\\{2,2<x<4}\\{2x-6,x≥4}\end{array}\right.$.分x≤2时,;2<x<4,x≥4,解f(x)>2.
(2))由|x-4|+|x-2|≥2,得M=2,由2x+a≥M的解集包含[0,1],得20+a≥2,21+a≥2
解答 解:(1)f(x)=|x-4|+|x-2|=$\left\{\begin{array}{l}{6-2x.x≤2}\\{2,2<x<4}\\{2x-6,x≥4}\end{array}\right.$.
∴当x≤2时,f(x)>2,6-2x>2,解得x<2;
当2<x<4时,f(x)>2得2>2,无解;
当x≥4时,f(x)>2得2x-6>2,解得>4.
所以不等式f(x)>2的解集为(-∞,2)∪(4,+∞).
(2))∵|x-4|+|x-2|≥2,∴M=2,
∵2x+a≥M的解集包含[0,1],
∴20+a≥2,21+a≥2,∴a≥1.
故a的取值范围为:[1,+∞)
点评 本题考查了绝对值不等式的解法,及恒成立问题,属于中档题.

练习册系列答案
相关题目
4.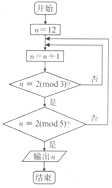 若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=4(mod7),如图所示的程序框图的算法源于我国古代闻名中外的《中国剩余定理》,执行该程序框图,则输出的n=( )
若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=4(mod7),如图所示的程序框图的算法源于我国古代闻名中外的《中国剩余定理》,执行该程序框图,则输出的n=( )
 若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=4(mod7),如图所示的程序框图的算法源于我国古代闻名中外的《中国剩余定理》,执行该程序框图,则输出的n=( )
若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=4(mod7),如图所示的程序框图的算法源于我国古代闻名中外的《中国剩余定理》,执行该程序框图,则输出的n=( )| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
1.运行如图所示的程序框图,输出的结果S=( )


| A. | 14 | B. | 30 | C. | 62 | D. | 126 |
19.如图是用二分法求方程x3-2=0近似解的算法的程序框图,则①②两处应依次填入( )


| A. | a=m,b=m | B. | b=m,a=m | C. | a=f(m),b=f(m) | D. | b=f(m),a=f(m) |