题目内容
20.已知p:x∈$\left\{{x\left|{\frac{x+2}{x-10}≤0}\right.}\right\}$,q:x∈{x|x2-2x+1-m2<0,m>0},若p是q的必要不充分条件,求实数m的取值范围.分析 分别求出根据p,q的x的范围,根据p是q的必要不充分条件,得到(1-m,1+m)?[-2,10),求出m的范围即可.
解答 解:p:x∈$\left\{{x\left|{\frac{x+2}{x-10}≤0}\right.}\right\}$,故p:x∈{x|-2≤x<10},
q:x∈{x|x2-2x+1-m2<0,m>0},故q:{x|1-m<x<1+m},
若p是q的必要不充分条件,
则(1-m,1+m)?[-2,10),
故$\left\{\begin{array}{l}{1-m>-2}\\{1+m<10}\end{array}\right.$,解得:m<3,
又m>0,
故m∈(0,3).
点评 本题考查了充分必要条件,考查集合的包含关系以及不等式问题,是一道基础题.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
10.已知点O为△ABC所在平面内一点,${\overrightarrow{OA}^2}={\overrightarrow{OB}^2}={\overrightarrow{OC}^2}$,若$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}$,且$|{\overrightarrow{AC}}|=|{\overrightarrow{AO}}|$,则$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
15.将一枚均匀硬币先后抛两次,恰好有一次出现正面的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
5.函数y=Asin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数的一个表达式为( )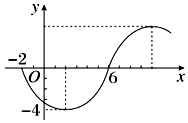

| A. | y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$) | B. | y=4sin($\frac{π}{8}$x-$\frac{π}{4}$) | C. | y=-4sin($\frac{π}{8}$x-$\frac{π}{4}$) | D. | y=4sin($\frac{π}{8}$x+$\frac{π}{4}$) |
10.已知等比数列{an}中,各项都是正数,且${a_1},\frac{1}{2}{a_3},2{a_2}$成等差数列,则$\frac{{{a_{10}}}}{a_8}$=( )
| A. | $\sqrt{2}$ | B. | $3-2\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $\sqrt{3}$ |
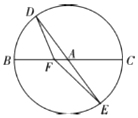 如图,BC是单位圆A的一条直径,F是线段AB上的点,且$\overrightarrow{BF}$=3$\overrightarrow{FA}$,若DE是圆A中绕圆心A运动的一条直径,则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值是$-\frac{15}{16}$.
如图,BC是单位圆A的一条直径,F是线段AB上的点,且$\overrightarrow{BF}$=3$\overrightarrow{FA}$,若DE是圆A中绕圆心A运动的一条直径,则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值是$-\frac{15}{16}$.