题目内容
18.若椭圆C1:$\frac{{x}^{2}}{{{a}_{1}}^{2}}$+$\frac{{y}^{2}}{{{b}_{1}}^{2}}$=1(a1>b1>0)和椭圆C2:$\frac{{x}^{2}}{{{a}_{2}}^{2}}$+$\frac{{y}^{2}}{{{b}_{2}}^{2}}$=1(a2>b2>0)的焦点相同且a1>a2.给出如下四个结论:①椭圆C1与椭圆C2一定没有公共点
②$\frac{{a}_{1}}{{a}_{2}}$>$\frac{{b}_{1}}{{b}_{2}}$
③a12-a22=b12-b22
④a1-a2=b1-b2
其中所有正确结论的序号是( )
| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
分析 先由a12-b12=a22-b22,从而③a12-a22=b12-b22成立,下面从两个方面来看:一方面:a1>a2,由上得b1>b2,从而①成立;②不成立;另一方面:a12-b12=a22-b22⇒(a1+b1)(a1-b1)=(a2+b2)(a2-b2)⇒a1-b1<a2-b2,从而④成立;从而得出正确答案.
解答 解:由a12-b12=a22-b22,从而③a12-a22=b12-b22成立,
一方面:a1>a2,由上得b1>b2,从而①成立;
若在a12-a22=b12-b22中,a1=2,a2=$\sqrt{2}$,b1=$\sqrt{3}$,b2=1,
$\frac{{a}_{1}}{{a}_{2}}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,$\frac{{b}_{1}}{{b}_{2}}$=$\frac{\sqrt{3}}{1}$=$\sqrt{3}$,有:$\frac{{a}_{1}}{{a}_{2}}$<$\frac{{b}_{1}}{{b}_{2}}$,
故②不成立;
另一方面:a12-b12=a22-b22,(a1+b1)(a1-b1)=(a2+b2)(a2-b2)
由于a1+b1>a2+b2
∴a1-b1<a2-b2,
从而④成立;
∴所有正确结论的序号是 ①③④.
故选B.
点评 本题主要考查椭圆的简单性质、椭圆的标准方程、不等式的性质等基础知识,考查运算求解能力,考查转化思想.属于基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
13.若log3a<log3b<0,则( )
| A. | 0<b<a<1 | B. | 0<a<b<1 | C. | b>a>1 | D. | a>b>1 |
3.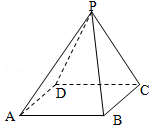 如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )
如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )
 如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )
如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )| A. | 4 | B. | 8 | C. | 12π | D. | 16π |
10.已知等比数列{an}中,各项都是正数,且${a_1},\frac{1}{2}{a_3},2{a_2}$成等差数列,则$\frac{{{a_{10}}}}{a_8}$=( )
| A. | $\sqrt{2}$ | B. | $3-2\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $\sqrt{3}$ |
7.已知实数x,y满足ax<ay(0<a<1),则下列关系式恒成立的是( )
| A. | $\frac{1}{{{x^2}+1}}>\frac{1}{{{y^2}+1}}$ | B. | ln(x2+1)>ln(y2+1) | C. | sinx>siny | D. | x3>y3 |
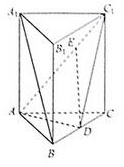 在正三棱柱ABC-A1B1C1中,点D为BC的中点;
在正三棱柱ABC-A1B1C1中,点D为BC的中点;