题目内容
在R上可导的函数f(x)=
x3+
ax2+2bx+c,当x∈(0,1)时取得极大值,当x∈(1,2)时取得极小值,则
的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
| b-3 |
| a-1 |
A、(
| ||||
B、(-
| ||||
C、(
| ||||
D、(
|
考点:函数在某点取得极值的条件
专题:函数的性质及应用
分析:据极大值点左边导数为正右边导数为负,极小值点左边导数为负右边导数为正得a,b的约束条件,据线性规划求出最值.
解答:
 解∵f′(x)=x2+ax+2b,
解∵f′(x)=x2+ax+2b,
∵函数f(x)在区间(0,1)内取得极大值,在区间(1,2)内取得极小值,
∴f′(x)=x2+ax+2b=0在(0,1)和(1,2)内各有一个根,
f′(0)>0,f′(1)<0,f′(2)>0,
即
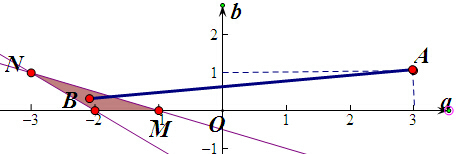
,在aOb坐标系中画出其表示的区域,如
表示点A(3,1)与可行域内的点B连线的斜率,
当B(x,y)=M(-1,0)时,
最大,最大为
;
当B(x,y)=N(-3,1)时,
最小,最小为
,
∴
的取值范围(
,
),
故选:A
 解∵f′(x)=x2+ax+2b,
解∵f′(x)=x2+ax+2b,∵函数f(x)在区间(0,1)内取得极大值,在区间(1,2)内取得极小值,
∴f′(x)=x2+ax+2b=0在(0,1)和(1,2)内各有一个根,
f′(0)>0,f′(1)<0,f′(2)>0,
即
|
| b-3 |
| a-1 |
当B(x,y)=M(-1,0)时,
| b-3 |
| a-1 |
| 3 |
| 2 |
当B(x,y)=N(-3,1)时,
| b-3 |
| a-1 |
| 1 |
| 2 |
∴
| b-3 |
| a-1 |
| 1 |
| 2 |
| 3 |
| 2 |
故选:A
点评:考查学生利用导数研究函数极值的能力,以及会进行简单的线性规划的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
已知命题p:存在x0∈R,使得2x0=1.则¬p是( )
| A、任给x0∈R,有2x0≠1 |
| B、任给x0∉R,有2x0≠1 |
| C、存在x0∈R,使得2x0≠1 |
| D、存在x0∉R,使得2x0≠1 |
对于函数y=f(x),以下说法正确的有( )
①y是x的函数;②对于不同的x值,y值也不同;③函数是一种对应,是多对一或一对一,不是一对多.
①y是x的函数;②对于不同的x值,y值也不同;③函数是一种对应,是多对一或一对一,不是一对多.
| A、①② | B、①③ | C、②③ | D、①②③ |
设向量
=(1,5,-1),
=(-2,2,4),若(k
-
)⊥
,则k=( )
| a |
| b |
| a |
| b |
| b |
| A、-4 | B、-6 | C、4 | D、6 |
已知向量
=(2,k),
=(1,2),若
⊥
,则k的值为( )
| a |
| b |
| a |
| b |
| A、-1 | B、1 | C、4 | D、-4 |
已知数列{an}满足a1=2,an+1=2an+2n+2,则an=( )
| A、n•2n+1 |
| B、(n+1)•2n+1 |
| C、(2n+1)•2n |
| D、(2n-1)•2n |
 如图,AB是圆O直径,CD⊥AB,过点C的切线与BA的延长线相交于点P.若AB=6,CD=2
如图,AB是圆O直径,CD⊥AB,过点C的切线与BA的延长线相交于点P.若AB=6,CD=2