题目内容
20.已知函数f(x)=$\frac{2sin2x+cos4x-1}{2sin2x}$.(1)求函数f(x)的定义域;
(2)化简函数式,并求出函数f(x)的值域.
分析 (1)要使f(x)=$\frac{2sin2x+cos4x-1}{2sin2x}$有意义,则sin2x≠0,解得即可,
(2)根据二倍角公式,化简,再根据正弦函数的图象和性质即可求出值域.
解答 解:(1)要使f(x)=$\frac{2sin2x+cos4x-1}{2sin2x}$有意义,
则sin2x≠0,即2x≠kπ,即x≠$\frac{kπ}{2}$,k∈Z,
故函数的定义域为{x|x≠$\frac{kπ}{2}$,k∈Z},
(2)f(x)=$\frac{2sin2x+cos4x-1}{2sin2x}$=1+$\frac{1-si{n}^{2}2x-1}{2sin2x}$=1-$\frac{1}{2}$sin2x,
∵-1≤sin2x≤1,且sin2x≠0,
∴$\frac{1}{2}$≤1-$\frac{1}{2}$sin2x≤$\frac{3}{2}$,且1-$\frac{1}{2}$sin2x≠1,
故函数f(x)的值域为[$\frac{1}{2}$,1)∪(1,$\frac{3}{2}$].
点评 本题考查了函数的定义域和值域的问题,以及二倍角公式,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
11.在正六边形ABCDEF中,若AB=1,则|$\overrightarrow{AB}$+$\overrightarrow{FE}$+$\overrightarrow{CD}$|等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.三对夫妻站成一排照相,则仅有一对夫妻相邻的站法总数是( )
| A. | 72 | B. | 144 | C. | 240 | D. | 288 |
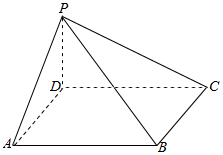 如图所示,四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠DAB=60°,PA=PB=PD=a.
如图所示,四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠DAB=60°,PA=PB=PD=a.