题目内容
11.在正六边形ABCDEF中,若AB=1,则|$\overrightarrow{AB}$+$\overrightarrow{FE}$+$\overrightarrow{CD}$|等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 可作出图形,并连接AD,可以得到$|\overrightarrow{AB}+\overrightarrow{FE}+\overrightarrow{CD}|=|\overrightarrow{AD}|$,取AD的中点O,并连接OC,从而可以得到AD=2AB=2.
解答 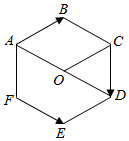 解:如图,连接AD;
解:如图,连接AD;
$|\overrightarrow{AB}+\overrightarrow{FE}+\overrightarrow{CD}|=|\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}|$=$|\overrightarrow{AD}|$;
取AD的中点O,连接CO,则四边形ABCO为菱形,△OCD为等边三角形,且AB=1;
∴AD=2;
∴$|\overrightarrow{AB}+\overrightarrow{FE}+\overrightarrow{CD}|=2$.
故选:B.
点评 考查对正六边形的认识,相等向量的概念,向量加法的几何意义,以及菱形的概念.

练习册系列答案
相关题目
1.设x,y满足约束条件$\left\{{\begin{array}{l}{x≥1}\\{x-2y≤0}\\{y-2≤0}\end{array}}\right.$,则z=x+2y-3的最大值为( )
| A. | 8 | B. | 5 | C. | 2 | D. | 1 |
19.已知a∈[0,2π),函数f(x)=cos$\frac{1}{2}$(x+a)是奇函数,则a的值为( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | π | D. | $\frac{3π}{2}$ |
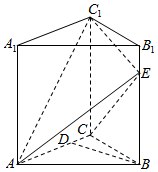 如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=2$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上一点,BD∥平面AC1E.
如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=2$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上一点,BD∥平面AC1E.