题目内容
15.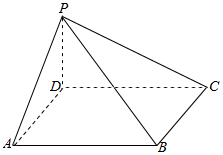 如图所示,四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠DAB=60°,PA=PB=PD=a.
如图所示,四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠DAB=60°,PA=PB=PD=a.(I)求证:PB⊥BC;
(Ⅱ)求二面角A-PB-C的余弦值.
分析 (I)根据线面垂直的性质即可证明PB⊥BC;
(Ⅱ)利用向量法,表示出向量$\overrightarrow{AC}$=$\overrightarrow{AH}$+$\overrightarrow{HB}$+$\overrightarrow{BC}$,得到向量$\overrightarrow{HA}$与$\overrightarrow{BC}$所成的角即可二面角A-PB-C的平面角,根据向量关系即可求二面角A-PB-C的余弦值.
解答  解:(I)∵底面ABCD是边长为a的菱形,∠DAB=60°,
解:(I)∵底面ABCD是边长为a的菱形,∠DAB=60°,
∴取AD的中点E,则BE⊥AD,
∵PA=PD=a,∴PE⊥AD,
∵PE∩AD=E,
∴AD⊥平面PBE,
∵AD∥BC,
∴BC⊥平面PBE
∵PB?平面PBE,
∴PB⊥BC.
(Ⅱ)∵底面ABCD是边长为a的菱形,∠DAB=60°,
∴AB=a,AC=$\sqrt{3}$a,
则△PAB是正三角形,
取PB的中点H,
则AH⊥PB,
∵PB⊥BC.
∴向量$\overrightarrow{HA}$与$\overrightarrow{BC}$所成的角即可二面角A-PB-C的平面角,
∵BH=$\frac{1}{2}$a,AH=$\frac{\sqrt{3}}{2}$a,
$\overrightarrow{AC}$=$\overrightarrow{AH}$+$\overrightarrow{HB}$+$\overrightarrow{BC}$,
∴$\overrightarrow{AC}$2=($\overrightarrow{AH}$+$\overrightarrow{HB}$+$\overrightarrow{BC}$)2=$\overrightarrow{AH}$2+$\overrightarrow{HB}$2+$\overrightarrow{BC}$2+2$\overrightarrow{AH}$•$\overrightarrow{HB}$+2$\overrightarrow{AH}$•$\overrightarrow{BC}$+2$\overrightarrow{HB}$•$\overrightarrow{BC}$,
即3a2=$\frac{3}{4}$a2+$\frac{1}{4}$a2+a2+0-2×$\frac{\sqrt{3}}{2}$a•acos<$\overrightarrow{HA}$,$\overrightarrow{BC}$>即cos<$\overrightarrow{HA}$,$\overrightarrow{BC}$>=$-\frac{\sqrt{3}}{3}$,
则二面角A-PB-C的余弦值是$-\frac{\sqrt{3}}{3}$.
点评 本题主要考查线面垂直的应用以及二面角的求解,利用向量法是解决本题的关键.综合性较强,有一定的难度.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案| A. | $\frac{3}{2}$ | B. | 3 | C. | 6 | D. | 8 |
| A. | f(x)=lgx+lg(x-1),g(x)=lg[x(x-1)] | B. | f(x)=$\frac{\sqrt{1-{x}^{2}}}{|x+2|-2}$,g(x)=$\frac{\sqrt{1-{x}^{2}}}{x}$ | ||
| C. | y=f(x)与y=f(x-3) | D. | f(x)=|x|+|x-1|,g(x)=2x-1 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 不存在 |
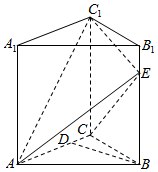 如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=2$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上一点,BD∥平面AC1E.
如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=2$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上一点,BD∥平面AC1E.