题目内容
已知函数f(x)=sinx+sin(x+
),x∈R.
(Ⅰ) 求f(x)的单调递增区间;
(Ⅱ) 若f(α)=
,求sin2α的值.
| π |
| 2 |
(Ⅰ) 求f(x)的单调递增区间;
(Ⅱ) 若f(α)=
| 3 |
| 4 |
考点:两角和与差的正弦函数,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:(1)先根据两角和与差的正弦公式进行化简,再由正弦函数的单调性可得到-
+2kπ≤x+
≤
+2kπ,进而可求出x的范围,再结合题中所给x的范围确定答案.
(2)利用同角三角函数的基本关系式以及二倍角公式直接求解即可.
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
(2)利用同角三角函数的基本关系式以及二倍角公式直接求解即可.
解答:
解:(1)∵f(x)=sinx+sin(x+
)=sinx+cosx=
sin(x+
),
令-
+2kπ≤x+
≤
+2kπ,
∴-
+2kπ≤x≤
+2kπ,k∈Z.f(x)的单调递增区间[
+2kπ,
+2kπ].k∈Z.
(2).∵f(α)=
,∴sinx+cosx=
,
∴2sinxcosx=-
,sin2α=-
.
| π |
| 2 |
| 2 |
| π |
| 4 |
令-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
∴-
| 3π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
(2).∵f(α)=
| 3 |
| 4 |
| 3 |
| 4 |
∴2sinxcosx=-
| 7 |
| 16 |
| 7 |
| 16 |
点评:本题主要考查两角和与差的正弦公式和正弦函数的单调性的应用.二倍角公式的应用,考查基础知识的灵活应用.高考中三角函数的考查一般以基础为主,要强化基础的夯实,属基础题.

练习册系列答案
相关题目
已知(x,y)满足
,则k=
的最大值等于( )
|
| y |
| x+1 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
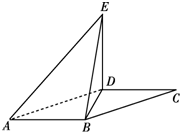 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4.将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4.将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.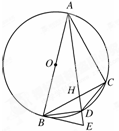 如图,AB是⊙O的直径,BE为⊙O的切线,点C为⊙O上不同于A,B的一点,AD为∠BAC的平分线,且分别与BC交于H,与⊙O交于D,与BE交于E,连接BD,CD.
如图,AB是⊙O的直径,BE为⊙O的切线,点C为⊙O上不同于A,B的一点,AD为∠BAC的平分线,且分别与BC交于H,与⊙O交于D,与BE交于E,连接BD,CD.