题目内容
平面内给定三个向量a＝(3,2)，b＝(－1,2)，c＝(4,1)，请解答下列问题：
(1)求满足a＝mb＋nc的实数m、n；
(2)若(a＋kc)∥(2b－a)，求实数k；
(3)若d满足(d－c)∥(a＋b)，且|d－c|＝
，求d.
(1)由题意得(3,2)＝m(－1,2)＋n(4,1)，
所以
得
(2)a＋kc＝(3＋4k,2＋k)，2b－a＝(－5,2)，
∵(a＋kc)∥(2b－a)，
∴2×(3＋4k)－(－5)×(2＋k)＝0，
∴k＝－
.
(3)设d＝(x，y)，则d－c＝(x－4，y－1)，a＋b＝(2,4)，
由题意得
解得
或
∴d＝(3，－1)或d＝(5,3)．
练习册系列答案
名校课堂系列答案
相关题目
asinC－ccosA.
，则△PBC与△ABC的面积之比是________．
CE与BF相交于G点．若
，则
＝( )
a＋
b B.
b
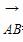a＋
＝a，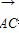
＝b，a·b<0，S△ABC＝
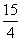，|a|＝3，|b|＝5，则∠BAC等于( )
，cos(B＋C))，A、B、C为△ABC的内角，其所对的边分别为a、b、c.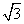
时，求b2＋c2的取值范围．