题目内容
已知a、b、c分别为△ABC三个内角A、B、C的对边,c= asinC-ccosA.
asinC-ccosA.
(1)求A;
(2)若a=2,△ABC的面积为 ,求b、c.
,求b、c.
(1)由c= asinC-ccosA及正弦定理得,
asinC-ccosA及正弦定理得,
 sinAsinC-cosAsinC-sinC=0.
sinAsinC-cosAsinC-sinC=0.
由于sinC≠0,所以sin(A-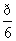 )=
)= .
.
又0<A<π,故A=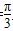 .
.
(2)△ABC的面积S= bcsinA=
bcsinA= ,故bc=4.
,故bc=4.
而a2=b2+c2-2bccosA,故b2+c2=8.
解得b=c=2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 B.
B.
 D.
D. ,且
,且 =-27.
=-27. m B.100
m B.100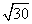 m D.30m
m D.30m ,1),b=(0,-1),c=(k,
,1),b=(0,-1),c=(k, ,求d.
,求d.