题目内容
13.已知指数函数y=f(x)的图象过点P(3,27),则在(0,10]内任取一个实数x,使得f(x)>81的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{7}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
分析 设函数f(x)=ax,a>0 且a≠1,把点(3,27),求得a的值,可得函数的解析式,进而结合几何概型可得到答案
解答 解:设函数f(x)=ax,a>0 且a≠1,
把点(3,27),代入可得 a3=27,
解得a=3,
∴f(x)=3x.
又∵x∈(0,10],
若f(x)>81,则x∈(4,10],
∴f(x)>81的概率P=$\frac{10-4}{10-0}$=$\frac{3}{5}$,
故选:D.
点评 本题主要考查用待定系数法求函数的解析式,几何概型,是函数和概率的综合应用.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
4.已知全集U={l,2,3,4,5},集合A={2,3,4},B={l,4}则(∁UA)∩B为( )
| A. | {1} | B. | {1,5} | C. | {1,4} | D. | {1,4,5} |
18.已知线性回归直线方程是$\stackrel{∧}{y}$=1.23x+0.08,求m的值.
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | m | 6.5 | 7.0 |
2.若O为△ABC内一点,且2$\overrightarrow{OA}$$+7\overrightarrow{OB}$$+6\overrightarrow{OC}$=$\overrightarrow{0}$,三角形ABC的面积是三角形OAB面积的λ倍,则λ=( )
| A. | $\frac{5}{2}$ | B. | $\frac{15}{2}$ | C. | $\frac{15}{7}$ | D. | 5 |
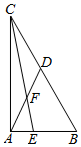 已知$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}-\overrightarrow{AC}$|=2,D是边BC的中点,$\overrightarrow{AE}$=$\frac{1}{3}\overrightarrow{AB}$
已知$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}-\overrightarrow{AC}$|=2,D是边BC的中点,$\overrightarrow{AE}$=$\frac{1}{3}\overrightarrow{AB}$