题目内容

4．等比数列{an}各项均为正数且a5a6=8，则log2a1+log2a2+…+log2a10=（　　）
A．15B．10C．12D．4+log25

分析 利用等比数列的性质可得：等比数列{an}各项均为正数且a5a6=8=a1a10=…=8，再利用对数的运算性质即可得出．

解答 解：∵等比数列{an}各项均为正数，
∴a5a6=8=a1a10=…=8，
则log2a1+log2a2+…+log2a10=log2（a1a2•…•a10）=$lo{g}_{2}（{a}_{5}{a}_{6}）^{5}$=$lo{g}_{2}{8}^{5}$=15．
故选：A．

点评 本题考查了等比数列的性质、对数的运算性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
14．已知椭圆C的右焦点F（1，0），过F的直线l与椭圆C交于A，B两点，当l垂直于x轴时，|AB|=3．
（1）求椭圆C的标准方程；
（2）在x轴上是否存在点T，使得$\overrightarrow{TA}$•$\overrightarrow{TB}$为定值？若存在，求出点T坐标，若不存在，说明理由．
15．实数x，y满足$\left\{\begin{array}{l}x+y≥3\\ x-y≥-1\\ 2x-y≤3\end{array}\right.$，则$\frac{{{x^2}+{y^2}}}{xy}$的取值范围是[2，$\frac{5}{2}$]．
12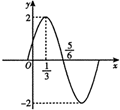．已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象（部分）如图所示，则要得到y=f（x）的图象，只需要把y=Asinωx的图象（　　）
A．向左平移$\frac{π}{6}$个单位B．向右平移$\frac{π}{6}$个单位
C．向左平移$\frac{1}{6}$个单位D．向右平移$\frac{1}{6}$个单位
19．数列$\frac{1}{1×2}，-\frac{1}{2×3}，\frac{1}{3×4}，-\frac{1}{4×5}，…$的通项公式an=（-1）n+1•$\frac{1}{n（n+1）}$．
9．掷一枚骰子，观察掷出的点数，则事件“掷出奇数点或3的倍数”的概率为$\frac{2}{3}$．
16．计算：
（1）lg14-2lg$\frac{7}{3}$+lg7-lg18
（2）（2$\frac{7}{9}$）0.5+（0.1）-2+（2$\frac{10}{27}$）${\;}^{-\frac{2}{3}}$-3π0+$\frac{37}{48}$．
13．已知A（-2，0）、B（2，0），P（2，4），动点满足$\overrightarrow{MA}$•$\overrightarrow{MB}$=0，M的轨迹为曲线C．
（1）求动点M的轨迹方程；
（2）过P作曲线C的切线，求切线的方程．
17．若不等式x2+a|x|+1≥0对x∈[-$\frac{1}{2}$，$\frac{1}{2}}$]恒成立，则实数a的取值范围是（　　）
A．[-2，+∞）B．[-2，2]C．（-∞，-2]D．[-$\frac{5}{2}$，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网