题目内容
11. 如图所示,四棱锥P-ABCD中平面PAB⊥平面ABCD,底面ABCD是正方形.点M是棱PC的中点
如图所示,四棱锥P-ABCD中平面PAB⊥平面ABCD,底面ABCD是正方形.点M是棱PC的中点(1)记平面ADM与平面PBC的交线是l,试判断直线l与BC的位置关系,并加以证明.
(2)若$PA=AB=1,PB=\sqrt{2}$,求证PB⊥平面ADM,并求直线PC与平面ADM所成角的正弦值.
分析 (1)证明AD∥平面PBC,利用线面平行的性质可得AD∥l,由平行公理即可得出l∥BC;
(2)建立空间坐标系,利用向量法证明PB⊥AD,PB⊥AM,故而PB⊥平面ADM,计算$\overrightarrow{PB}$,$\overrightarrow{PC}$的夹角即可得出直线PC与平面ADM所成角的正弦值.
解答 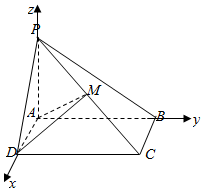 解:(1)∵四边形ABCD是正方形,
解:(1)∵四边形ABCD是正方形,
∴AD∥BC,
又AD?平面PBC,BC?平面PBC,
∴AD∥平面PBC,
又AD?平面ADM,平面ADM∩平面PBC=l,
∴AD∥l,
又AD∥BC,
∴l∥BC.
(2)证明:以A为原点建立空间直角坐标系,
则P(0,0,1),B(0,1,0),D(1,0,0),C(1,1,0),M($\frac{1}{2}$,$\frac{1}{2}$,$\frac{1}{2}$),
∴$\overrightarrow{PB}$=(0,1,-1),$\overrightarrow{AD}$=(1,0,0),$\overrightarrow{AM}$=($\frac{1}{2}$,$\frac{1}{2}$,$\frac{1}{2}$),
∴$\overrightarrow{PB}$$•\overrightarrow{AD}$=0,$\overrightarrow{PB}•\overrightarrow{AM}$=0,
∴PB⊥AD,PB⊥AM,
又AD?平面ADM,AM?平面ADM,AD∩AM=A,
∴PB⊥平面ADM.
∴$\overrightarrow{PB}$=(0,1,-1)是平面ADM的一个法向量,
又$\overrightarrow{PC}$=(1,1,-1),
∴cos<$\overrightarrow{PB},\overrightarrow{PC}$>=$\frac{\overrightarrow{PB}•\overrightarrow{PC}}{|\overrightarrow{PB}||\overrightarrow{PC}|}$=$\frac{2}{\sqrt{2}•\sqrt{3}}$=$\frac{\sqrt{6}}{3}$.
∴直线PC与平面ADM所成角的正弦值为$\frac{\sqrt{6}}{3}$.
点评 本题考查了线面平行的判定与性质,线面角的计算,属于中档题.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 充分而不必要 | B. | 必要而不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |