��Ŀ����
8����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������M��1��$\frac{3}{2}$������������Ϊ$\frac{1}{2}$����1������ԲC�ķ��̣�
��2����ֱ��l��y=kx+m��m��0��|k|��$\frac{1}{2}$������ԲC�ཻ��A��B���㣬���߶�OA��OBΪ�ڱ���ƽ���ı���OAPB�����ж���P����ԲC�ϣ�OΪ����ԭ�㣮��m��ȡֵ��Χ��
���� ��1������Բ��������e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{1}{2}$�������ã�3a2=4b2�����ٽ������M��1��$\frac{3}{2}$����������Բ���̼������a��b��ֵ�������ԲC�ķ��̣�
��2����k��Ҫ��k=0��k��0����������ۣ�����k=0ʱ��������⣻k��0ʱ����Ҫ����Բ���̺�ֱ�߷��������õ�����x�Ķ��η��̣���ƽ���ı���OAPB�У�$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$���ɴ˼��ɵõ�����������ϵ����حOPح=$\sqrt{{x}_{0}^{2}+{y}_{0}^{2}}$=$\sqrt{\frac{64{k}^{2}{m}^{2}}{��3+4{k}^{2}��^{2}}+\frac{36{m}^{2}}{��3+4{k}^{2}��^{2}}}$����k����ʾ��������k�ķ�Χ����ȷ��حOPح��ȡֵ��Χ��
��� �⣺��1������֪�ɵã�����Բ��������e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{1}{2}$�������ã�3a2=4b2����
�ֵ�M��1��$\frac{3}{2}$��������ԲC�ϣ�
��$\frac{1}{{a}^{2}}+\frac{9}{4{b}^{2}}=1$��
�ɢ٢ڽ�ã�a2=4��b2=3��
����ԲC�ķ���Ϊ��$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$��
��2����k=0ʱ��P��0��2m������ԲC�ϣ���ã�m=��$\frac{\sqrt{3}}{2}$��
��حOPح=$\sqrt{3}$��
��k��0ʱ����$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$��
��ȥy�����������ã���3+4k2��x2+8kmx+4m2-12=0��
��=64k2m2-4��3+4k2����4m2-12��=48��3+4k2-m2����0����
��A��B��P�������ֱ�Ϊ��x1��y1������x2��y2������x0��y0����
��Τ�ﶨ����֪��x1+x2=-$\frac{8km}{3+4{k}^{2}}$
�������߶�OA��OBΪ�ڱ���ƽ���ı���OAPB��
��x0=x1+x2=-$\frac{8km}{3+4{k}^{2}}$��y0=y1+y2=k��x1+x2��+2m=$\frac{6m}{3+4{k}^{2}}$��
���ڵ�P����ԲC�ϣ�
��$\frac{{x}_{0}^{2}}{4}+\frac{{y}_{0}^{2}}{3}=1$��
�Ӷ�$\frac{16{k}^{2}{m}^{2}}{��3+4{k}^{2}��^{2}}$+$\frac{12{m}^{2}}{��3+4{k}^{2}��^{2}}$=1��
����ã�4m2=3+4k2�������������ʽ��
��حOPح=$\sqrt{{x}_{0}^{2}+{y}_{0}^{2}}$=$\sqrt{\frac{64{k}^{2}{m}^{2}}{��3+4{k}^{2}��^{2}}+\frac{36{m}^{2}}{��3+4{k}^{2}��^{2}}}$��
=$\sqrt{\frac{4{m}^{2}��16{k}^{2}+9��}{��3+4{k}^{2}��^{2}}}$��
=$\sqrt{\frac{16{k}^{2}+9}{4{k}^{2}+3}}$��
=$\sqrt{4-\frac{3}{4{k}^{2}+3}}$��
��0��|k|��$\frac{1}{2}$��
��3��4k2+3��4����$\frac{3}{4}$��$\frac{3}{4{k}^{2}+3}$��1��
��$\sqrt{3}$��حOPح��$\frac{\sqrt{13}}{2}$��
���ϣ�حOPح��ȡֵ��Χ��[$\sqrt{3}$��$\frac{\sqrt{13}}{2}$]��
���� ���⿼����Բ�ı����̣�����ֱ������Բ��λ�ù�ϵ�����������������ʾ�������������˼�룬���������������е��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | 20x=M | B�� | 20x=M��1+5%��20 | C�� | 20x��M��1+5%��20 | D�� | 20x��M��1+5%��20 |
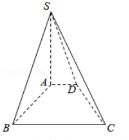 ��֪����S-ABCD�У�����ABCD��ֱ�����Σ���ABC=90�㣬AD��BC��SA=AB=BC=2��AD=1��SA�͵���ABCD��
��֪����S-ABCD�У�����ABCD��ֱ�����Σ���ABC=90�㣬AD��BC��SA=AB=BC=2��AD=1��SA�͵���ABCD��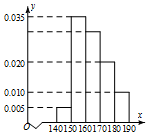 ij�����꼶��500��ͬѧ�������ǵ����ߣ���λ��cm�����ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ������������[160��170����[170��180����[180��190]�����ڵ�ѧ���У��÷ֲ�����ķ���ѡȡ30�˲μ�һ�������������[160��170���ڵ�ѧ����ѡȡ������ӦΪ15��
ij�����꼶��500��ͬѧ�������ǵ����ߣ���λ��cm�����ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ������������[160��170����[170��180����[180��190]�����ڵ�ѧ���У��÷ֲ�����ķ���ѡȡ30�˲μ�һ�������������[160��170���ڵ�ѧ����ѡȡ������ӦΪ15��