题目内容
3.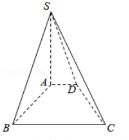 已知四棱锥S-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,SA=AB=BC=2,AD=1,SA⊥底面ABCD.
已知四棱锥S-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,SA=AB=BC=2,AD=1,SA⊥底面ABCD.(1)求四棱锥S-ABCD的体积;
(2)求异面直线SC与AD所成角的余弦值.
分析 (1)先求出S梯形ABCD,由此能求出四棱锥S-ABCD的体积.
(2)以A为原点,AB为x轴,AD为y轴,AS为z轴,建立空间直角坐标系,利用向量法能求出异面直线SC与AD所成角的余弦值.
解答 解:(1)∵四棱锥S-ABCD中,底面ABCD是直角梯形,
∠ABC=90°,AD∥BC,SA=AB=BC=2,AD=1,SA⊥底面ABCD,
∴S梯形ABCD=$\frac{1}{2}$(1+2)×2=3,
∴四棱锥S-ABCD的体积V=$\frac{1}{3}×{S}_{梯形ABCD}×SA$=$\frac{1}{3}×3×2$=2.
(2)以A为原点,AB为x轴,AD为y轴,AS为z轴,建立空间直角坐标系,
C(2,2,0),S(0,0,2),A(0,0,0),D(0,1,0),
$\overrightarrow{SC}$=(2,2,-2),$\overrightarrow{AD}$=(0,1,0),
设异面直线SC与AD所成角为θ,
则cosθ=$\frac{|\overrightarrow{SC}•\overrightarrow{AD}|}{|\overrightarrow{SC}|•|\overrightarrow{AD}|}$=$\frac{2}{\sqrt{12}}$=$\frac{\sqrt{3}}{3}$.
∴异面直线SC与AD所成角的余弦值为$\frac{\sqrt{3}}{3}$.
点评 本题考查四棱锥的体积的求法,考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
13.函数f(x)=(x-3)ex的单调增区间是( )
| A. | (-∞,2) | B. | (2,+∞) | C. | (1,4) | D. | (0,3) |
11.函数f(x)=$\sqrt{3}$x+2cosx,x∈(0,π)上单调减区间为( )
| A. | ($\frac{π}{3}$,$\frac{2π}{3}$) | B. | ($\frac{π}{6}$,$\frac{5π}{6}$) | C. | (0,$\frac{π}{3}$),($\frac{2π}{3}$,π) | D. | (0,$\frac{π}{6}$),($\frac{5π}{6}$,π) |
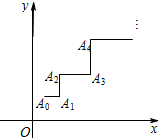 一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图,A0(x0,y0)的坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.
一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图,A0(x0,y0)的坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.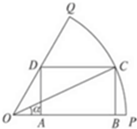 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,四边形ABCD是扇形的内接矩形,记∠COP=α,矩形的面积为S;
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,四边形ABCD是扇形的内接矩形,记∠COP=α,矩形的面积为S;