题目内容

20．求下列函数的定义域，并用区间表示其结果．
（1）y=$\sqrt{x+2}$+$\frac{2x+1}{{x}^{2}-x-6}$；
（2）y=$\frac{\sqrt{4-x}}{1-|x-2|}$．

分析 （1）根据函数y的解析式，列出使解析式有意义的不等式组$\left\{\begin{array}{l}{x+2≥0}\\{{x}^{2}-x-6≠0}\end{array}\right.$，求出解集即可；
（2）根据函数y的解析式，列出不等式组$\left\{\begin{array}{l}{4-x≥0}\\{1-|x-2|≠0}\end{array}\right.$，求出解集即可．

解答 解：（1）∵y=$\sqrt{x+2}$+$\frac{2x+1}{{x}^{2}-x-6}$，
∴$\left\{\begin{array}{l}{x+2≥0}\\{{x}^{2}-x-6≠0}\end{array}\right.$，
解得x≥-2且x≠-2且x≠3，
∴函数y的定义域是（-2，3）∪（3，+∞）；
（2）∵y=$\frac{\sqrt{4-x}}{1-|x-2|}$，
∴$\left\{\begin{array}{l}{4-x≥0}\\{1-|x-2|≠0}\end{array}\right.$，
解得x≤4且x≠1且x≠3，
∴函数y的定义域是（-∞，1）∪（1，3）∪（3，4]．

点评 本题考查了根据函数解析式求定义域的应用问题，是基础题目．

练习册系列答案
相关题目
10．函数f（x）=$\frac{3}{2}$x2-lnx的极值点为$\frac{\sqrt{3}}{3}$．
11．函数f（x）=$\sqrt{3}$x+2cosx，x∈（0，π）上单调减区间为（　　）
A．（$\frac{π}{3}$，$\frac{2π}{3}$）B．（$\frac{π}{6}$，$\frac{5π}{6}$）C．（0，$\frac{π}{3}$），（$\frac{2π}{3}$，π）D．（0，$\frac{π}{6}$），（$\frac{5π}{6}$，π）
8．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点M（1，$\frac{3}{2}$），其离心率为$\frac{1}{2}$．
（1）求椭圆C的方程；
（2）设直线l：y=kx+m（m≠0，|k|≤$\frac{1}{2}$）与椭圆C相交于A、B两点，以线段OA，OB为邻边作平行四边形OAPB，其中顶点P在椭圆C上，O为坐标原点．求m的取值范围．
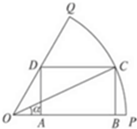15．如图，已知OPQ是半径为1，圆心角为$\frac{π}{3}$的扇形，C是扇形弧上的动点，四边形ABCD是扇形的内接矩形，记∠COP=α，矩形的面积为S；
（1）求出S与α的函数关系式，并指出α的取值范围；
（2）求S最大值．
5．下列程序执行后输出的结果是（　　）
A．3B．6C．15D．10
12．已知函数f（x）=3（x-2）2+5，且|x1-2|＞|x2-2|，则f（x1），f（x2）的大小关系是f（x1）＞f（x2）．
9．在直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系，已知直线l的参数方程为$\left\{\begin{array}{l}{x=-1+t}\\{y=1+t}\end{array}\right.$，（t为参数），曲线C的普通方程为（x-2）2+（y-1）2=5，点P的极坐标为（2$\sqrt{2}$，$\frac{7π}{4}$）．
（1）求直线l的普通方程和曲线C的极坐标方程；
（2）若将直线l向右平移2个单位得到直线l′，设l′与C相交于A，B两点，求△PAB的面积．
10．已知f（x）=$\frac{4^x}{{{4^x}+{2}}}$，x∈R．
（1）求证：对一切实数x，f（x）=f（1-x）恒为定值．
（2）计算：f（-6）+f（-5）+f（-4）+f（-3）+…+f（0）+…+f（6）+f（7）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网