题目内容
18.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$过点P(4,2),且它的渐近线与圆${({x-2\sqrt{2}})^2}+{y^2}=\frac{8}{3}$相切,则该双曲线的方程为( )| A. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{8}=1$ | C. | $\frac{x^2}{8}-\frac{y^2}{12}=1$ | D. | $\frac{x^2}{12}-\frac{y^2}{12}=1$ |
分析 利用双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$过点P(4,2),且它的渐近线与圆${({x-2\sqrt{2}})^2}+{y^2}=\frac{8}{3}$相切,建立方程,求出a,b,即可求出双曲线的方程.
解答 解:由题意,$\left\{\begin{array}{l}{\frac{16}{{a}^{2}}-\frac{4}{{b}^{2}}=1}\\{\frac{|2\sqrt{2}b|}{\sqrt{{b}^{2}+{a}^{2}}}=\sqrt{\frac{8}{3}}}\end{array}\right.$,
∴a=2$\sqrt{2}$,b=2,
∴双曲线的方程为$\frac{{x}^{2}}{8}-\frac{{y}^{2}}{4}$=1,
故选A.
点评 本题考查了双曲线的标准方程及简单的几何性质,直线与圆相切的条件,以及点到直线的距离公式,考查方程思想,化简、计算能力.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
8.若对于定义在R上的函数f(x)当且仅当存在有限个非零自变量x,使得f(-x)=f(x),则称f(x)为类偶函数,若函数f(x)=x3+(a2-2a)x+a为类偶函数,则f(a)的取值范围为( )
| A. | (0,2) | B. | (-∞,0]∪[2,+∞) | C. | [0,2] | D. | (-∞,0]∪(2,+∞) |
9.复数z=$\frac{2-i}{1+2i}$,则$\overline{z}$=( )
| A. | i | B. | 1+i | C. | -i | D. | 1-i |
3.在正方体ABCD-A1B1C1D1中,异面直线A1B与AD1所成角的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
10.sin$\frac{5π}{3}$的值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
7.已知函数y=f(x)的图象如图所示,则y=f(x)的解析式可能是( )


| A. | y=2x-x2-x | B. | y=$\frac{{2}^{x}sinx}{4x+1}$ | C. | y=(x2-2x)ex | D. | y=$\frac{x}{lnx}$ |
8.函数y=ln|x|-x2的图象大致为( )
| A. | 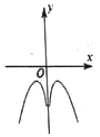 | B. | 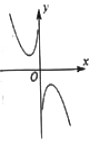 | C. |  | D. | 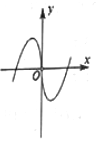 |