题目内容
已知等差数列{an}的首项a1=2,a7=4a3,前n项和为Sn.
(Ⅰ)求an及Sn;
(Ⅱ)设bn=
,n∈N*,求bn的最大值.
(Ⅰ)求an及Sn;
(Ⅱ)设bn=
| Sn-4an-4 |
| n |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件利用等差数列的通项公式求出公差,由此能求出an=-3n+5,Sn=
.
(Ⅱ) 由(I)得bn=
=
-
(n+
).由基本不等式能求出bn的最大值.
| -3n2+7n |
| 2 |
(Ⅱ) 由(I)得bn=
| Sn-4an-4 |
| n |
| 21 |
| 2 |
| 3 |
| 2 |
| 16 |
| n |
解答:
满分(14分).
解:(Ⅰ) 设公差为d,由题意知
a1+6d=4(a1+2d),
由a1=2解得d=-3,
故an=-3n+5,Sn=
,n∈N*.…(8分)
(Ⅱ) 由(I)得
bn=
=
-
(n+
).
由基本不等式得
n+
≥2
=8,
所以bn=
-
(n+
)≤
,又当n=4时,bn=
.
从而得bn的最大值为
.…(14分)
解:(Ⅰ) 设公差为d,由题意知
a1+6d=4(a1+2d),
由a1=2解得d=-3,
故an=-3n+5,Sn=
| -3n2+7n |
| 2 |
(Ⅱ) 由(I)得
bn=
| Sn-4an-4 |
| n |
| 31 |
| 2 |
| 3 |
| 2 |
| 16 |
| n |
由基本不等式得
n+
| 16 |
| n |
n•
|
所以bn=
| 31 |
| 2 |
| 3 |
| 2 |
| 16 |
| n |
| 7 |
| 2 |
| 7 |
| 2 |
从而得bn的最大值为
| 7 |
| 2 |
点评:本题主要考查等差数列的概念与通项公式、求和公式、不等式等基础知识,同时考查运算求解能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

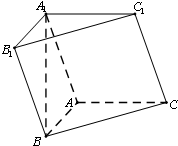 如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B.
如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B.