题目内容
9．直线3x+4y-2=0和直线6x+8y+1=0的距离是（ ）| A． | $\frac{3}{5}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{10}$ | D． | $\frac{1}{5}$ |
分析 直线6x+8y-4=0和直线6x+8y+1=0，代入两平行线间的距离公式，即可得到答案．
解答 解：由题意可得：3x+4y-2=0和直线6x+8y+1=0，
即直线6x+8y-4=0和直线6x+8y+1=0，
结合两平行线间的距离公式得：
两条直线的距离是d=$\frac{|-4-1|}{\sqrt{36+64}}$=$\frac{1}{2}$，
故选：B．
点评 先把两平行直线的对应变量的系数化为相同的，再利用两平行线间的距离公式求出两平行线间的距离．
练习册系列答案
相关题目
17．在直角坐标系中，点P坐标是（-3，3），以原点为极点，x轴正半轴为极轴建立的极坐标系中，点P的极坐标是（ ）
| A． | $（{3\sqrt{2}，\frac{3π}{4}}）$ | B． | $（{3\sqrt{2}，\frac{5π}{4}}）$ | C． | $（{3，\frac{5π}{4}}）$ | D． | $（{3，\frac{3π}{4}}）$ |
14．
已知某几何体的三视图如图所示，其中俯视图是腰长为2的等腰梯形，则该几何体的全面积为（ ）
已知某几何体的三视图如图所示，其中俯视图是腰长为2的等腰梯形，则该几何体的全面积为（ ）| A． | $40+6\sqrt{3}$ | B． | $40+12\sqrt{3}$ | C． | 12$\sqrt{3}$ | D． | 24$\sqrt{3}$ |
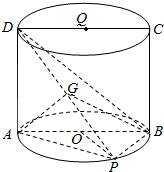如图，四边形ABCD是体积为8$\sqrt{3}$π的圆柱OQ的轴截面，点P在底面圆周上，BP=OA=2，G是DP的中点．