��Ŀ����
4����ƽ��ֱ������ϵxOy�У�ԲC�IJ�������Ϊ$\left\{\begin{array}{l}x=2sint\\ y=2cost\end{array}\right.����tΪ������$������ԭ��OΪ���㣬x��ķǸ�����Ϊ���Ὠ���ļ�����ϵ�У�ֱ��l�ļ����귽��Ϊ$��sin����+\frac{��}{4}��=2\sqrt{2}$��A��2��0��������ԲC����ͨ���̺�ֱ��l��ֱ�����귽�̣�
���� AP��ԲC�϶��ң���AP�е�M��l�������Сֵ��
���� �����������ַ��̵�ת����������ԲC����ͨ���̺�ֱ��l��ֱ�����귽�̣�
���� ��P��2cos����2sin��������M��cos��+1��sin���������õ㵽ֱ�ߵľ��빫ʽ���������߶�AP���е�M��ֱ��l�ľ������Сֵ��
��� �⣺������ȥ�����ã�ԲC����ͨ���̵�x2+y2=4�� ֱ��l�ļ����귽��Ϊ$��sin����+\frac{��}{4}��=2\sqrt{2}$��ֱ�����귽��Ϊx+y-4=0��
������P��2cos����2sin��������M��cos��+1��sin������
��d=$\frac{|cos��+sin��-3|}{\sqrt{2}}$=$\frac{|\sqrt{2}sin����+45�㣩-3|}{\sqrt{2}}$��
����Сֵ��$\frac{3-\sqrt{2}}{\sqrt{2}}$=$\frac{3\sqrt{2}-2}{2}$������10�֣�
���� ���⿼��������̡���ͨ���̡������귽�̵�ת��������㵽ֱ�ߵľ��빫ʽ������ѧ���ļ��������������е��⣮

��ϰ��ϵ�д�
�����Ŀ
9��ֱ��3x+4y-2=0��ֱ��6x+8y+1=0�ľ����ǣ�������
| A�� | $\frac{3}{5}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{3}{10}$ | D�� | $\frac{1}{5}$ |
16�� ��ͼ����ֱ������ABC-A1B1C1�У�AB=BC=2$\sqrt{2}��C{C_1}$=4����ABC=90�㣬E��F�ֱ�ΪAA1��C1B1���е㣬�������ı���ӵ�E����F�����·���ij���Ϊ��������
��ͼ����ֱ������ABC-A1B1C1�У�AB=BC=2$\sqrt{2}��C{C_1}$=4����ABC=90�㣬E��F�ֱ�ΪAA1��C1B1���е㣬�������ı���ӵ�E����F�����·���ij���Ϊ��������
 ��ͼ����ֱ������ABC-A1B1C1�У�AB=BC=2$\sqrt{2}��C{C_1}$=4����ABC=90�㣬E��F�ֱ�ΪAA1��C1B1���е㣬�������ı���ӵ�E����F�����·���ij���Ϊ��������
��ͼ����ֱ������ABC-A1B1C1�У�AB=BC=2$\sqrt{2}��C{C_1}$=4����ABC=90�㣬E��F�ֱ�ΪAA1��C1B1���е㣬�������ı���ӵ�E����F�����·���ij���Ϊ��������| A�� | $\sqrt{14+4\sqrt{2}}$ | B�� | $\sqrt{22}$ | C�� | $3\sqrt{2}$ | D�� | $2\sqrt{3}$ |
13����֪$f��x��=3sin��{��x+\frac{��}{6}}����{�أ�0}��$����f��x��ͼ������ƽ��$\frac{��}{6}$����λ��ͼ����y=3cos��xͼ���غϣ�
��1����ص���Сֵ��
��2����������1���½��±����ݲ������������á���㷨������f��x����һ�������ڵ�ͼ��
��1����ص���Сֵ��
��2����������1���½��±����ݲ������������á���㷨������f��x����һ�������ڵ�ͼ��
| $��x+\frac{��}{6}$ | 0 | $\frac{��}{2}$ | �� | $\frac{3��}{2}$ | 2�� |
| x | |||||
| f��x�� |
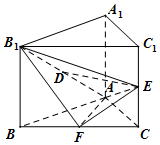 ��ֱ֪������ABC-A1B1C1�У���ABCΪ����ֱ�������Σ���BAC=90�㣬��AB=AA1��D��E��F�ֱ�ΪB1A��C1C��BC���е㣮
��ֱ֪������ABC-A1B1C1�У���ABCΪ����ֱ�������Σ���BAC=90�㣬��AB=AA1��D��E��F�ֱ�ΪB1A��C1C��BC���е㣮