题目内容
6.已知直线方程y=$\sqrt{3}$x+2,则该直线的倾斜角为$\frac{π}{3}$.分析 直线方程y=$\sqrt{3}$x+2,设该直线的倾斜角为θ,θ∈[0,π).则tanθ=$\sqrt{3}$,即可得出.
解答 解:直线方程y=$\sqrt{3}$x+2,设该直线的倾斜角为θ,θ∈[0,π).
则tanθ=$\sqrt{3}$,∴θ=$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查了直线的斜率与倾斜角的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
5.已知函数f(x)=$\sqrt{3}$sinωxcosωx+sin2ωx(ω>0)的最小正周期为π,将函数f(x)的图象向右平移φ(φ>0)个单位后,得到的函数关于点(-$\frac{π}{4}$,$\frac{1}{2}$)对称,则φ的值不可能为( )
| A. | $\frac{π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{7π}{3}$ |
14.已知函数y=sin(ωx+$\frac{π}{3}$)向右平移$\frac{π}{3}$个单位后,所得的图象与原函数图象关于x轴对称,则ω的最小正值为( )
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
11.如图所示,正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,以下四个结论中正确的是( )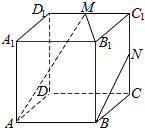

| A. | 直线MN与DC1互相垂直 | B. | 直线AM与BN互相平行 | ||
| C. | 直线MN与BC1所成角为90° | D. | 直线MN垂直于平面A1BCD1 |
18.已知变量x与y负相关,且由观测数据算得样本平均数$\overline{x}$=4,$\overline{y}$=2.5,则由该观测数据算得的线性回归方程可能是( )
| A. | $\widehat{y}$=0.4x+0.9 | B. | $\widehat{y}$=2x-5.5 | C. | $\widehat{y}$=-2x+10.5 | D. | $\widehat{y}$=-0.3x+4.7 |
15.函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1,x≥0}\\{g(x)+a,x<0}\end{array}\right.$为奇函数,若g(-2)=4,则a=( )
| A. | -3 | B. | 4 | C. | -7 | D. | 6 |
16.已知a,b是两条不重合的直线,α,β是两个不同的平面,则下列命题中正确的是( )
| A. | 若a⊥b,a⊥α,则b∥α | B. | 若a⊥α,b∥α,则a⊥b | ||
| C. | 若a∥b,b?α,则a∥α | D. | 若a,b?α,a∥β,b∥β,则α∥β |