题目内容
11.如图所示,正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,以下四个结论中正确的是( )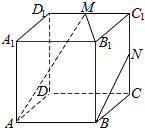
| A. | 直线MN与DC1互相垂直 | B. | 直线AM与BN互相平行 | ||
| C. | 直线MN与BC1所成角为90° | D. | 直线MN垂直于平面A1BCD1 |
分析 在A中,由MN∥D1C,D1C⊥DC1,得直线MN与DC1互相垂直,故A正确;在B中,直线AM与BN相交;在C中:直线MN与BC1所成角为60°;在D中,MN∥平面A1BCD1.
解答 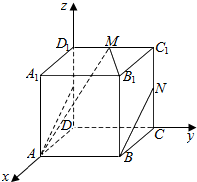 解:在A中:∵正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,
解:在A中:∵正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,
∴MN∥D1C,
在B中:∵D1C⊥DC1,∴直线MN与DC1互相垂直,故A正确;
取DD1中点E,连结AE,则BN∥AE,由AE∩AM=A,得直线AM与BN相交,故B错误;
在C中:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为2,
则M(0,1,2),N(0,2,1),B(2,2,0),C1(0,2,2),
$\overrightarrow{MN}$=(0,1,-1),$\overrightarrow{B{C}_{1}}$=(-2,0,2),
cos<$\overrightarrow{MN},\overrightarrow{B{C}_{1}}$>=$\frac{\overrightarrow{MN}•\overrightarrow{B{C}_{1}}}{|\overrightarrow{MN}|•|\overrightarrow{B{C}_{1}}|}$=$\frac{-2}{\sqrt{2}×\sqrt{8}}$=-$\frac{1}{2}$,
∴直线MN与BC1所成角为60°,故C错误;
在D中:∵$\overrightarrow{MN}$=(0,1,-1),A1(2,0,2),$\overrightarrow{{A}_{1}B}$=(0,2,-2),
∴$\overrightarrow{MN}$∥$\overrightarrow{{A}_{1}B}$,∵MN?平面A1BCD1,A1B?平面A1BCD1,
∴MN∥平面A1BCD1,故D错误.
故选:A.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意向量法的合理运用.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案| A. | 6 | B. | $\sqrt{3}$(1+$\sqrt{2}$+$\sqrt{3}$) | C. | 3+3$\sqrt{2}$ | D. | 3+3$\sqrt{3}$ |
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 线性回归直线方程y=bx+a恒过样本中心$(\overline x,\overline y)$,且至少经过一个样本点 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
| A. | $\sqrt{3}$ | B. | $\sqrt{10}$ | C. | 3 | D. | 2 |
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -1 | D. | 1 |
| A. | [$\sqrt{2}$,+∞) | B. | [2,+∞) | C. | (0,2] | D. | [-$\sqrt{2}$,-1]∪[$\sqrt{2}$,$\sqrt{3}$] |
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | -$\frac{1}{2}$ |
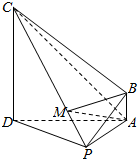 在四梭推 P-ABCD中,CD⊥平面PAD,AB∥CD,CD=4AB,AC⊥PA,M为线段CP上一点.
在四梭推 P-ABCD中,CD⊥平面PAD,AB∥CD,CD=4AB,AC⊥PA,M为线段CP上一点.