题目内容
1.已知函数f(x)=x2+ax+3-a,a∈R.(1)求a的取值范围,使y=f(x)在闭区间[-1,3]上是单调函数;
(2)当0≤x≤2时,函数y=f(x)的最大值是关于a的函数M(a),求M(a).
分析 (1)函数f(x)=x2+ax+3-a图象的对称轴为$x=-\frac{a}{2}$,结合二次函数的性质可得$-\frac{a}{2}≤-1$或$-\frac{a}{2}≥3$,从而解得.
(2)由二次函数的性质知,讨论0,2与对称轴的距离,从而确定最大值即可.
解答 解:(1)函数f(x)=x2+ax+3-a图象的对称轴为$x=-\frac{a}{2}$,
∵f(x)在闭区间[-1,3]上是单调函数,
∴$-\frac{a}{2}≤-1$或$-\frac{a}{2}≥3$,
∴a≤-6或a≥2.
(2)当$-\frac{a}{2}≤1$,即a≥-2时,
由二次函数的性质可得,
M(a)=f(2)=7+a,
当-$\frac{a}{2}$>1,即a<-2时,
M(a)=f(0)=3-a,
故M(a)=$\left\{\begin{array}{l}{3-a,a<-2}\\{7+a,a≥-2}\end{array}\right.$.
点评 本题考查了二次函数的图象及性质应用,同时考查了分类讨论的思想应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.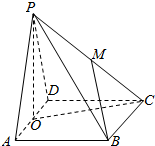 已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是边长为2的正三角形,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是( )
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是边长为2的正三角形,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是( )
 已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是边长为2的正三角形,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是( )
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是边长为2的正三角形,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{\sqrt{2}}{3}$ |
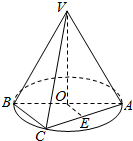 如图AB是圆O的直径,点C是圆O上不同于A,B的一点,点V是圆O所在平面外一点.
如图AB是圆O的直径,点C是圆O上不同于A,B的一点,点V是圆O所在平面外一点.