题目内容
14.已知函数y=sin(ωx+$\frac{π}{3}$)向右平移$\frac{π}{3}$个单位后,所得的图象与原函数图象关于x轴对称,则ω的最小正值为( )| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
分析 由三角函数图象变换可得后来函数的解析式,由诱导公式比较可得ω的方程,解方程给k取值可得.
解答 解:函数y=sin(ωx+$\frac{π}{3}$)向右平移$\frac{π}{3}$个单位后得到
y=sin[ω(x-$\frac{π}{3}$)+$\frac{π}{3}$]=sin(ωx-$\frac{π}{3}$ω+$\frac{π}{3}$)的图象,
∵所得的图象与原函数图象关于x轴对称,
∴sin(ωx-$\frac{π}{3}$ω+$\frac{π}{3}$)=-sin(ωx+$\frac{π}{3}$)=sin(ωx+$\frac{π}{3}$+π),
∴-$\frac{π}{3}$ω+$\frac{π}{3}$=$\frac{π}{3}$+π+2kπ,k∈Z,解得ω=-6k-3,
∴当k=-1时,ω取最小正数3,
故选:D.
点评 本题考查三角函数的图象和性质,涉及图象变换,属基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
5.已知函数f(x)=$\left\{\begin{array}{l}{x+4,x≥0}\\{x-4,x<0}\end{array}\right.$,当0<a<1时,则f(a-1)的值是( )
| A. | a+3 | B. | -a+5 | C. | a-5 | D. | -a-3 |
2.下列有关命题的说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 线性回归直线方程y=bx+a恒过样本中心$(\overline x,\overline y)$,且至少经过一个样本点 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
9.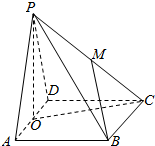 已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是边长为2的正三角形,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是( )
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是边长为2的正三角形,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是( )
 已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是边长为2的正三角形,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是( )
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是边长为2的正三角形,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{\sqrt{2}}{3}$ |
19.已知$\overrightarrow a,\overrightarrow b$满足:$\left|{\overrightarrow a}\right|=2,\left|{\overrightarrow b}\right|=1,\left|{\overrightarrow a-\overrightarrow b}\right|=\sqrt{6}$,则$\left|{\overrightarrow a+\overrightarrow b}\right|$( )
| A. | $\sqrt{3}$ | B. | $\sqrt{10}$ | C. | 3 | D. | 2 |