题目内容
18．已知变量x与y负相关，且由观测数据算得样本平均数$\overline{x}$=4，$\overline{y}$=2.5，则由该观测数据算得的线性回归方程可能是（ ）| A． | $\widehat{y}$=0.4x+0.9 | B． | $\widehat{y}$=2x-5.5 | C． | $\widehat{y}$=-2x+10.5 | D． | $\widehat{y}$=-0.3x+4.7 |
分析 根据负相关的回归方程的一次项系数为负，及样本数据中心点坐标为（4，2.5）利用排除法，可得答案．
解答 解：由已知中变量x与y负相关，
故回归方程的一次项系数为负，
故排除A，B，
由样本平均数$\overline{x}$=4，$\overline{y}$=2.5，
故回归直线过（4，2.5）点，
故排除D，
故选：C．
点评 本题考查的知识点是线性回归方程，正确理解正负相关与回归系数的关系，及回归直线方程必过样本数据中心点，是解答的关键．
练习册系列答案
相关题目
9．
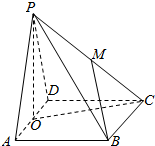已知四棱锥P-ABCD的底面ABCD是边长为2的正方形，侧面PAD是边长为2的正三角形，平面ABCD⊥平面PAD，M是PC的中点，O是AD的中点，则直线BM与平面PCO所成角的正弦值是（ ）
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形，侧面PAD是边长为2的正三角形，平面ABCD⊥平面PAD，M是PC的中点，O是AD的中点，则直线BM与平面PCO所成角的正弦值是（ ）| A． | $\frac{\sqrt{5}}{5}$ | B． | $\frac{2\sqrt{5}}{5}$ | C． | $\frac{1}{5}$ | D． | $\frac{\sqrt{2}}{3}$ |
3．已知O是锐角△ABC的外接圆圆心，∠A=60°，$\frac{cosB}{sinC}$•$\overrightarrow{AB}$+$\frac{cosC}{sinB}$•$\overrightarrow{AC}$=m•$\overrightarrow{OA}$，则m的值为（ ）
| A． | -$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | -1 | D． | 1 |
10．在8件获奖作品中，有3件一等奖，有5件二等奖，从这8件作品中任取3件．
（1）求取出的3件作品中，一等奖多于二等奖的概率；
（2）设X为取出的3件作品中一等奖的件数，求随机变量X的分布列和数学期望．
（1）求取出的3件作品中，一等奖多于二等奖的概率；
（2）设X为取出的3件作品中一等奖的件数，求随机变量X的分布列和数学期望．
7．某商场销售一种“艾丽莎”品牌服装，销售经理根据销售记录发现，该服装在过去的一个月内（以30天计）每件的销售价格P（x）（百元）与时间x（天）的函数关系近似满足P（x）=1+$\frac{k}{x}$（k为正的常数），日销售量Q（x）（件）与时间x（天）的部分数据如表所示：
已知第2哦天的日销售量为126百元．
（Ⅰ）求k的值；
（Ⅱ）给出以下三种函数模型：
①Q（x）=a•bx；
②Q（x）=a•logbx；
③Q（x）=a|x-25|+b．
请您根据如表中的数据，从中选择你认为最合适的一种函数来描述日销售量Q（x）（件）与时间x（天）的变化关系，并求出该函数的解析式；
（Ⅲ）求该服装的日销收入f（x）（1≤x≤30，x∈N*）（百元）的最小值．
| x（天） | 10 | 20 | 25 | 30 |
| Q（x）（件） | 110 | 120 | 125 | 120 |
（Ⅰ）求k的值；
（Ⅱ）给出以下三种函数模型：
①Q（x）=a•bx；
②Q（x）=a•logbx；
③Q（x）=a|x-25|+b．
请您根据如表中的数据，从中选择你认为最合适的一种函数来描述日销售量Q（x）（件）与时间x（天）的变化关系，并求出该函数的解析式；
（Ⅲ）求该服装的日销收入f（x）（1≤x≤30，x∈N*）（百元）的最小值．
8．若函数f（x）=21n（x+1）-1nax在其定义域内有且只有一个零点，则实数a的取值集合为（ ）
| A． | |4| | B． | （-∞，4] | C． | （-∞，0） | D． | （-∞，0）∪{4} |