题目内容
已知双曲线
-
=1
(1)过M(1,1)的直线交双曲线于A,B两点,若M 为AB的中点,求直线AB的方程.
(2)是否存在直线L,使N(1,
)为L被双曲线所截弦的中点,若存在,求出L的方程,若不存在,说明理由.
| x2 |
| 4 |
| y2 |
| 2 |
(1)过M(1,1)的直线交双曲线于A,B两点,若M 为AB的中点,求直线AB的方程.
(2)是否存在直线L,使N(1,
| 1 |
| 2 |
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)设过M(1,1)的直线方程为:y-1=k(x-1),A,B两点的坐标为(x1,y1),(x2,y2),代入双曲线方程,再相减,运用平方差公式和中点坐标公式,及斜率公式,即可得到所求直线的斜率,进而得到直线方程,检验判别式即可;
(2)假设存在直线l,使N(1,
)为l被双曲线所截弦的中点,则设弦CD的C、D两点的坐标为(x3,y3),(x4,y4),代入双曲线方程,再相减,运用平方差公式和中点坐标公式,及斜率公式,即可得到所求直线的斜率,进而得到直线方程,检验判别式的符号即可判断.
(2)假设存在直线l,使N(1,
| 1 |
| 2 |
解答:
解:(1)设过M(1,1)的直线方程为:y-1=k(x-1),
A,B两点的坐标为(x1,y1),(x2,y2),
则x12-2y12=4,x22-2y22=4,
相减可得,(x1-x2)(x1+x2)=2(y1-y2)(y1+y2)
由M为AB的中点,则x1+x2=2,y1+y2=2,
则k=
=
,
即有直线AB的方程:y-1=
(x-1),即有y=
x+
,
代入双曲线方程x2-2y2=4,检验判别式大于0,成立,
则所求直线方程为:有y=
x+
;
(2)假设存在直线l,使N(1,
)为l被双曲线所截弦的中点.
则设弦CD的C、D两点的坐标为(x3,y3),(x4,y4),
则x32-2y32=4,x42-2y42=4,
相减可得,(x3-x4)(x3+x4)=2(y3-y4)(y3+y4)
由N为CD的中点,则x3+x4=2,y3+y4=1,
则k=
=1,
则直线CD的方程为:y-
=x-1,即y=x-
,
代入双曲线方程x2-2y2=4,可得,x2-2x+
=0,
由于判别式为4-9<0,则该直线l不存在.
A,B两点的坐标为(x1,y1),(x2,y2),
则x12-2y12=4,x22-2y22=4,
相减可得,(x1-x2)(x1+x2)=2(y1-y2)(y1+y2)
由M为AB的中点,则x1+x2=2,y1+y2=2,
则k=
| y1-y2 |
| x1-x2 |
| 1 |
| 2 |
即有直线AB的方程:y-1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
代入双曲线方程x2-2y2=4,检验判别式大于0,成立,
则所求直线方程为:有y=
| 1 |
| 2 |
| 1 |
| 2 |
(2)假设存在直线l,使N(1,
| 1 |
| 2 |
则设弦CD的C、D两点的坐标为(x3,y3),(x4,y4),
则x32-2y32=4,x42-2y42=4,
相减可得,(x3-x4)(x3+x4)=2(y3-y4)(y3+y4)
由N为CD的中点,则x3+x4=2,y3+y4=1,
则k=
| y3-y4 |
| x3-x4 |
则直线CD的方程为:y-
| 1 |
| 2 |
| 1 |
| 2 |
代入双曲线方程x2-2y2=4,可得,x2-2x+
| 9 |
| 4 |
由于判别式为4-9<0,则该直线l不存在.
点评:本题考查双曲线的方程和运用,考查点差法求中点问题,注意检验判别式的符号,考查运算能力,属于中档题和易错题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
在平面直角坐标系中,设点P(x,y),定义[OP]=|x|+|y|,其中O为坐标原点.对于下列结论:
(1)符合[OP]=1的点P的轨迹围成的图形的面积为2;
(2)设点P是直线:
x+2y-2=0上任意一点,则[OP]min=1;
(3)设点P是直线:y=kx+1(k∈R)上任意一点,则“使得[OP]最小的点P有无数个”的充要条件是“k=±1”;
(4)设点P是圆x2+y2=1上任意一点,则[OP]max=
.
其中正确的结论序号为( )
(1)符合[OP]=1的点P的轨迹围成的图形的面积为2;
(2)设点P是直线:
| 5 |
(3)设点P是直线:y=kx+1(k∈R)上任意一点,则“使得[OP]最小的点P有无数个”的充要条件是“k=±1”;
(4)设点P是圆x2+y2=1上任意一点,则[OP]max=
| 2 |
其中正确的结论序号为( )
| A、(1)、(2)、(3) |
| B、(1)、(3)、(4) |
| C、(2)、(3)、(4) |
| D、(1)、(2)、(4) |
A是直二面角α-l-β的棱l上的一点,两条长为a的线段AB、AC分别在α、β内,且分别与l成45°角,则BC的长为( )
| A、a | ||||
B、a或
| ||||
C、
| ||||
D、a或
|
 如图,有一块边长为1km的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45° (其中点P,Q分别在边BC,CD上),设∠PAB=θ,tanθ=t
如图,有一块边长为1km的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45° (其中点P,Q分别在边BC,CD上),设∠PAB=θ,tanθ=t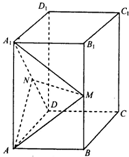 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.