题目内容
12．当双曲线：$\frac{{x}^{2}}{{m}^{2}+8}$-$\frac{{y}^{2}}{6-2m}$=1的焦距取得最小值时，其渐近线的斜率为（ ）| A． | ±1 | B． | $±\frac{2}{3}$ | C． | $±\frac{1}{3}$ | D． | $±\frac{1}{2}$ |
分析 由题意可得6-2m＞0，即有m＜3，由c2=m2+8+6-2m=（m-1）2+13，可得m=1取得最小值，由双曲线的渐近线方程，可得渐近线的斜率．
解答 解：由题意可得6-2m＞0，即有m＜3，
由c2=m2+8+6-2m=（m-1）2+13，
可得当m=1时，焦距2c取得最小值，
双曲线的方程为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1，
即有渐近线方程为y=±$\frac{2}{3}$x．
渐近线的斜率为±$\frac{2}{3}$x．
故选：B．
点评 本题考查双曲线的渐近线的斜率的求法，注意运用二次函数的最值的求法，考查运算能力，属于中档题．
练习册系列答案
相关题目
2．已知点F（-c，0）（c＞0）是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左焦点，过F作直线与圆x2+y2=a2相切，并与渐近线交于第一象限内一点P，满足|$\overrightarrow{OF}$|=|$\overrightarrow{OP}$|，则该双曲线的离心率等于（ ）
| A． | $\sqrt{5}$ | B． | 2 | C． | $\sqrt{3}$ | D． | $\frac{\sqrt{5}}{2}$ |
20．已知等差数列{an}的公差为2，若a1，a3，a4成等比数列，Sn是{an}的前n项和，则S9等于（ ）
| A． | -8 | B． | -6 | C． | 10 | D． | 0 |
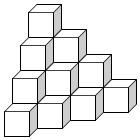如图所示，若每个小正方体的棱长为1cm．求
，
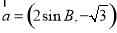且
．
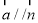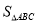的最大值．