题目内容
17．
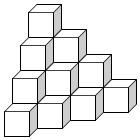如图所示，若每个小正方体的棱长为1cm．求①此几何体的体积V；
②此集合体的表面积S表面积．
分析 ①求出图中所有小正方体的个数，乘以1个小正方体的体积得答案；
②从几何体的左右、前后、上面查出裸漏的每一个小正方体的面，乘以一个小正方形的面积得答案．
解答 解：①由图可知，该几何体最上层由1个小正方体，第2层有3个小正方体，第3层有6个小正方体，第4层有10个小正方体．
则此几何体的体积V=（1+3+6+10）×13=20（cm3）；
②此集合体的表面积S表面积=（20+20+10+10+10）×12=70（cm2）．
点评 本题考查柱体的体积和表面积，考查空间想象能力和思维能力，是中档题．
练习册系列答案
相关题目
12．当双曲线：$\frac{{x}^{2}}{{m}^{2}+8}$-$\frac{{y}^{2}}{6-2m}$=1的焦距取得最小值时，其渐近线的斜率为（ ）
| A． | ±1 | B． | $±\frac{2}{3}$ | C． | $±\frac{1}{3}$ | D． | $±\frac{1}{2}$ |
2．已知F1，F2分别为双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点，若点P是以F1F2为直径的圆与C右支的-个交点，F1P交C于另一点Q，且|PQ|=2|QF1|．则C的渐近线方程为（ ）
| A． | y=±2x | B． | y=±$\frac{1}{2}$x | C． | y=±$\sqrt{2}$x | D． | y=±$\frac{\sqrt{2}}{2}$x |
6．函数f（x）=（1+$\sqrt{3}$tan2x）cos2x的最小正周期为（ ）
| A． | 2π | B． | $\frac{3π}{2}$ | C． | π | D． | $\frac{π}{2}$ |
中，
为平行四边形内一点，且
，若
，则
的最大值为 ．