题目内容
一名射手在一次射击中的得分情况是个随机变量，具体分布列为
（1）求b 的值；
（2）计算Y的期望与方差．
| Y | 0 | 1 | 2 |
| P | 0.2 | 0.2 | b |
（2）计算Y的期望与方差．
考点：离散型随机变量的期望与方差,离散型随机变量及其分布列
专题：概率与统计
分析：（1）利用离散型随机变量的分布列能求出b的值．
（2）利用（1）所得的分布列，结合数学期望和方差的计算公式求解即可．
（2）利用（1）所得的分布列，结合数学期望和方差的计算公式求解即可．
解答：
解：（1）由题意得：0.2+0.2+b=1，
解得b=0.6；
（2）Y的期望为：E（Y）=0×0.2+1×0.2+2×0.6=1.4，
Y的方差为：D（Y）=0.2×（0-1.4）2+0.2×（1-1.4）2+0.6×（2-1.4）2=0.64
解得b=0.6；
（2）Y的期望为：E（Y）=0×0.2+1×0.2+2×0.6=1.4，
Y的方差为：D（Y）=0.2×（0-1.4）2+0.2×（1-1.4）2+0.6×（2-1.4）2=0.64
点评：本题考查离散型随机变量的数学期望和方差，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
过点P（3，3）的直线l与线段MN相交，M（2，-3），N（-3，-2），则l的斜率k的取值范围为（ ）
A、
| ||||
B、
| ||||
C、k≤
| ||||
D、k≤
|
直线kx-y+1=0与圆（x-1）2+y2=4的位置关系是（ ）
| A、相交 | B、相切 |
| C、相离 | D、不确定，与k有关 |
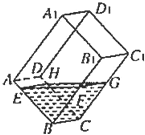如图，在透明材料制成的长方体容器ABCD-A1B1C1D1内灌注一些水，固定容器底面一边BC于桌面上，再将容器倾斜根据倾斜度的不同，有下列命题：