题目内容

10．已知复数z=$\frac{3+2i}{2-3i}$，则z的共轭复数$\overline z$=（　　）
A．1B．-1C．iD．-i

分析 直接利用复数代数形式的乘除运算化简，求得z，再由共轭复数的概念得答案．

解答 解：∵z=$\frac{3+2i}{2-3i}$=$\frac{（3+2i）（2+3i）}{（2-3i）（2+3i）}=\frac{13i}{13}=i$，
∴$\overline{z}=-i$，
故选：D．

点评 本题考查复数代数形式的乘除运算，考查了共轭复数的概念，是基础题．

练习册系列答案
相关题目
20．在区间[-4，4]上随机地取一个实数x，则事件“x2-2x-3≤0”发生的概率是$\frac{1}{2}$．
1．已知向量$\overrightarrow a$=（t，1）与$\overrightarrow b$=（4，t）共线且方向相同，则实数t=2．
18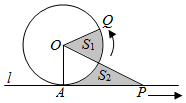．已知圆O与直线l相切于点A，点P，Q同时从A点出发，P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动，当Q运动到点A时，点P也停止运动，连接OQ，OP（如图），则阴影部分面积S1，S2的大小关系是（　　）
A．S1=S2B．S1≤S2
C．S1≥S2D．先S1＜S2，再S1=S2，最后S1＞S2
5．函数y=cos2x，x∈[0，π]的递增区间为[$\frac{π}{2}$，π]．
15．已知函数f（x）=sin（ωx+φ）（ω＞0），如果存在实数x0，使得对任意的实数x，都有f（x0）≤f（x）≤f（x0+2016π）成立，则ω的最小值为$\frac{1}{2016}$．
2．化简：
（1）1+2${C}_{n}^{1}$+4C${\;}_{n}^{2}$+…+2nC${\;}_{n}^{n}$；
（2）（x-1）5+5（x-1）4+10（x-1）3+10（x-1）2+5（x-1）．
19．满足|x|+|y|≤4的整点（横纵坐标均为整数）的点（x，y）的个数是（　　）
A．16B．17C．40D．41
20．若a＜0，则关于x的不等式x2-4ax-5a2＞0的解集是（　　）
A．（-∞，-a）∪（5a，+∞）B．（-∞，5a）∪（-a，+∞）C．（5a，-a）D．（a，-5a）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网