题目内容
已知双曲线过点(3,-2),且与椭圆4x2+9y2=36有相同的焦点.(Ⅰ)求双曲线的标准方程;
(Ⅱ)求以双曲线的右准线为准线的抛物线的标准方程.
【答案】分析:(I)先求出椭圆的焦点坐标,再根据双曲线的定理求出a,b,c,从而求出双曲线的方程;
(II)由(1)得双曲线的右准线方程,从而求出p,这样就可求出抛物线的标准方程.
解答:解:(I)由椭圆方程得焦点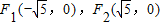 ,…(2分)
,…(2分)
由条件可知,双曲线过点(3,-2)
根据双曲线定义,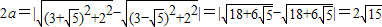 …(5分)
…(5分)
即得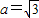 ,所以
,所以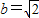 …(7分)
…(7分)
双曲线方程为: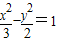 ,…(9分)
,…(9分)
(II)由(1)得双曲线的右准线方程为: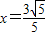 …(11分)
…(11分)
∴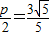 …(13分)
…(13分)
从而可得抛物线的标准方程为: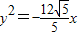 …(15分)
…(15分)
点评:本题主要考查了双曲线的标准方程,在求曲线方程的问题中,巧设方程,减少待定系数,是非常重要的方法技巧.特别是具有公共焦点的两种曲线,它们的公共点同时具有这两种曲线的性质,解题时要充分注意.
(II)由(1)得双曲线的右准线方程,从而求出p,这样就可求出抛物线的标准方程.
解答:解:(I)由椭圆方程得焦点
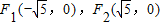 ,…(2分)
,…(2分)由条件可知,双曲线过点(3,-2)
根据双曲线定义,
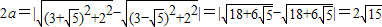 …(5分)
…(5分)即得
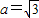 ,所以
,所以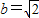 …(7分)
…(7分)双曲线方程为:
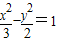 ,…(9分)
,…(9分)(II)由(1)得双曲线的右准线方程为:
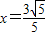 …(11分)
…(11分)∴
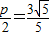 …(13分)
…(13分)从而可得抛物线的标准方程为:
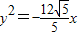 …(15分)
…(15分)点评:本题主要考查了双曲线的标准方程,在求曲线方程的问题中,巧设方程,减少待定系数,是非常重要的方法技巧.特别是具有公共焦点的两种曲线,它们的公共点同时具有这两种曲线的性质,解题时要充分注意.

练习册系列答案
相关题目