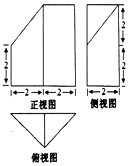
题目内容
10.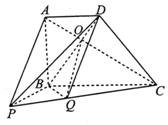 如图,在四棱锥P-ABCD中,ABCD是梯形,AD∥BC,∠ABC=90°,平面PAB⊥平面ABCD,PB⊥AB且AD=AB=BP=$\frac{1}{2}$BC.
如图,在四棱锥P-ABCD中,ABCD是梯形,AD∥BC,∠ABC=90°,平面PAB⊥平面ABCD,PB⊥AB且AD=AB=BP=$\frac{1}{2}$BC.(1)求证:CD⊥平面PBD;
(2)已知点Q在PC上,若AC与BD交于点O,且AP∥平面BDQ,求证:OQ∥平面APD.
分析 (1)证明CD⊥PB,CD⊥BD,即可证明CD⊥平面PBD;
(2)证明AP∥OQ,即可证明OQ∥平面APD.
解答 证明:(1)∵平面PAB⊥平面ABCD,PB⊥AB,平面PAB∩平面ABCD=AB,
∴PB⊥平面ABCD,
∵CD?平面ABCD,
∴CD⊥PB,
∵AD=AB=$\frac{1}{2}$BC,∠BAD=90°,
∴BD=$\sqrt{2}$AD,BC=2AD,∠DBC=45°,
∴∠BDC=90°,
∴CD⊥BD,
∵PB∩BD=B,
∴CD⊥平面PBD;
(2)∵AP∥平面BDQ,
∴AP∥OQ,
∵OQ?平面APD,AP?平面APD,
∴OQ∥平面APD.
点评 本题考查空间线面平行、垂直的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知对任意的a∈[-1,1],函数f(x)=x2+(a-4)x+4-2a的值总大于0,则x的取值范围是( )
| A. | x<1或x>3 | B. | 1<x<3 | C. | 1<x<2 | D. | x<2或x>3 |
2.已知点P(x,y)在不等式组$\left\{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}\right.$,表示的平面区域上运动,则z=x-y的取值范围是( )
| A. | [1,2] | B. | [-2,1] | C. | [-2,-1] | D. | [-1,2] |
20.已知关于x的一次函数y=mx+n,设m∈{-1,1,2},n∈{-2,2},则函数y=mx+n是增函数的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为$\frac{\sqrt{3}}{2}$,过C的左焦点F1,且垂直于x轴的直线被椭圆C截得的线段长为1.
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为$\frac{\sqrt{3}}{2}$,过C的左焦点F1,且垂直于x轴的直线被椭圆C截得的线段长为1.